BaekTree

Go Grow, Serve others.

3 minute read

mathBERT review

논문 mathBERT을 핵심 요약 정리한다.

이 글을 쓰는 2022년 1월 기준 동일한 이름의 mathBERT가 두개 있음. 중국의 peking univ에서 만든 mathBERT와 U-penn에서 만든 mathBERT가 있음. 근데 U-penn의 mathBERT 역시 1저자는 중국인이지만… 무튼 간략히 중국 버트와 미국 버트라고 부르면, 이 포스트는 중국 버트를 리뷰함.

중국 버트와 미국 버트의 공통점

기존의 버트는 자연어를 사전학습 했음. 두 mathBERT 모두 궁극적으로 지향하는 바는 똑같음. 수학 도메인에서 사전 학습된 버트 backbone 모델을 만들자!

차이점

지향하는 바가 조금 다르다. 미국 버트는 다양한 교과서 데이터들 기존의 버트를 가지고 와서 domain adaptation, task adaption을 사용해서 사전 학습 시킴. 결과적으로 DAPT가 더 효과가 좋았더라고 보고함. 중국 버트는 수식 자체에 조금 더 많은 관심을 가짐. 그래서 수식의 표현에도 관심을 가지고, 이 수식을 어떻게 모델이 인식하게 할까 고민했음. 그리고 수식을 설명하는 paragraph가 있을 때 context와 수식의 관계 등을 모델에 학습시키고 싶어했음.

DAPT와 TAPT는 이미 개념이 익숙하기 때문에, 수식 자체와 context와의 관계를 더 많이 고민한 중국 버트가 신선하고 흥미로워서 중국 버트를 리뷰함.

mathBERT 핵심 요약정리

저자

Shuai Peng, Ke Yuan, Liangcai Gao, Zhi Tang from Peking University

contribution

자연어만 아는 버트에 수식을 학습시킴. 이제 모델이 수식과 수식을 설명하는 글에 대한 관계를 이해하고, 특히 수식의 구조적 특징을 이해함.

결과

눈에 띄는 성능 향상을 보임

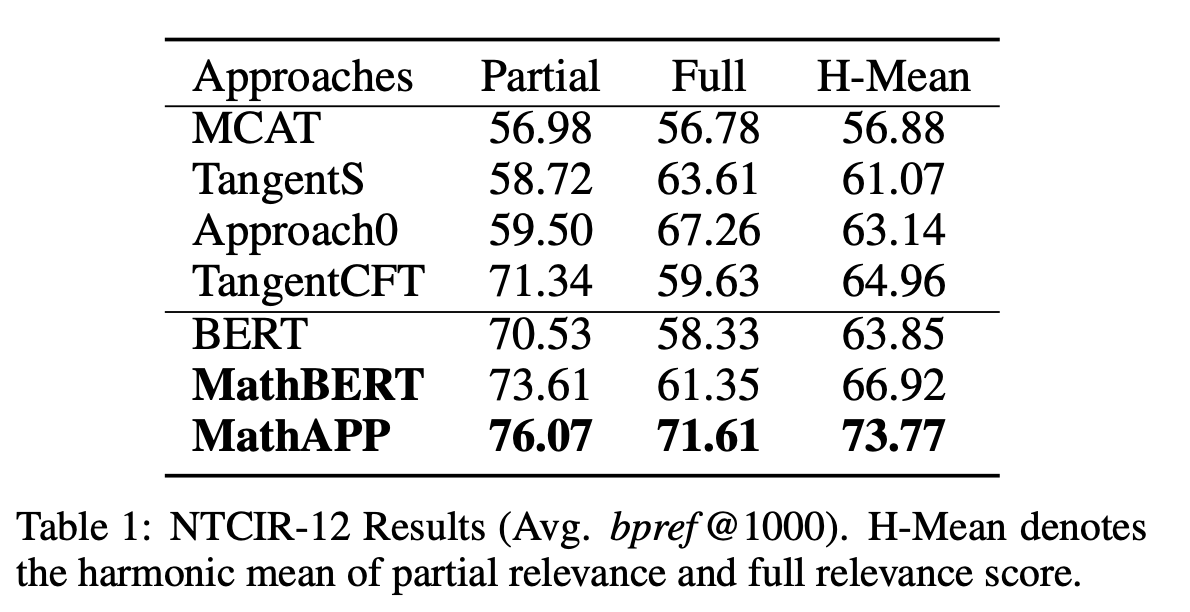
Untitled

mathBERT result such that given a formula as the query, mathematical information retrieval aims to return the relevance of formulas in a large set of document.

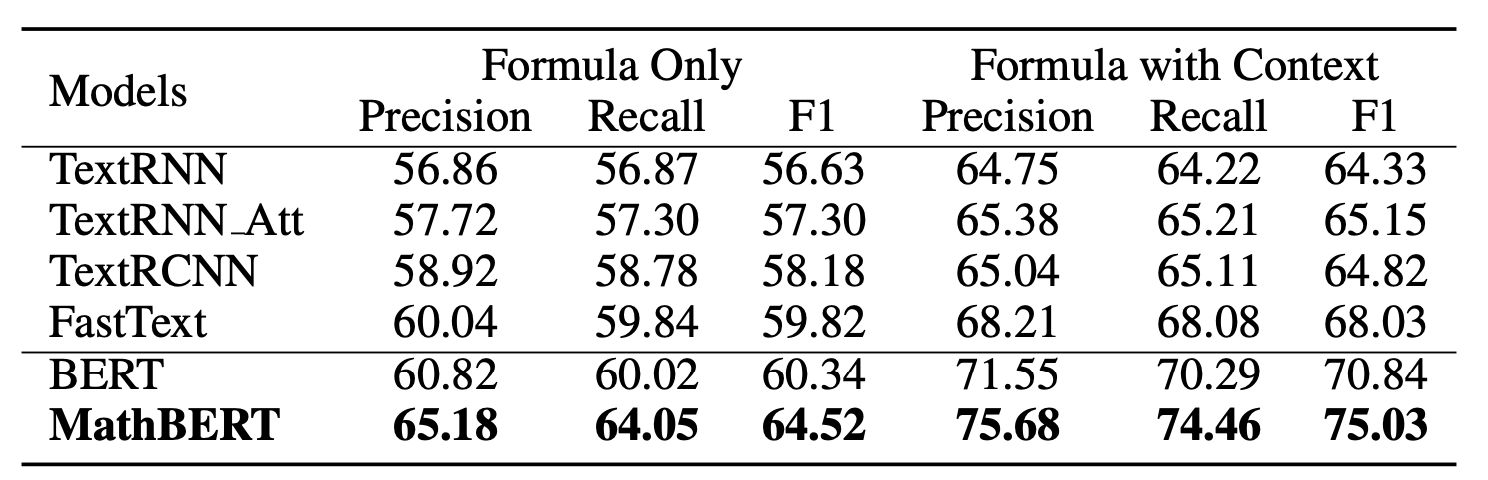
Untitled

Formula topic classification result

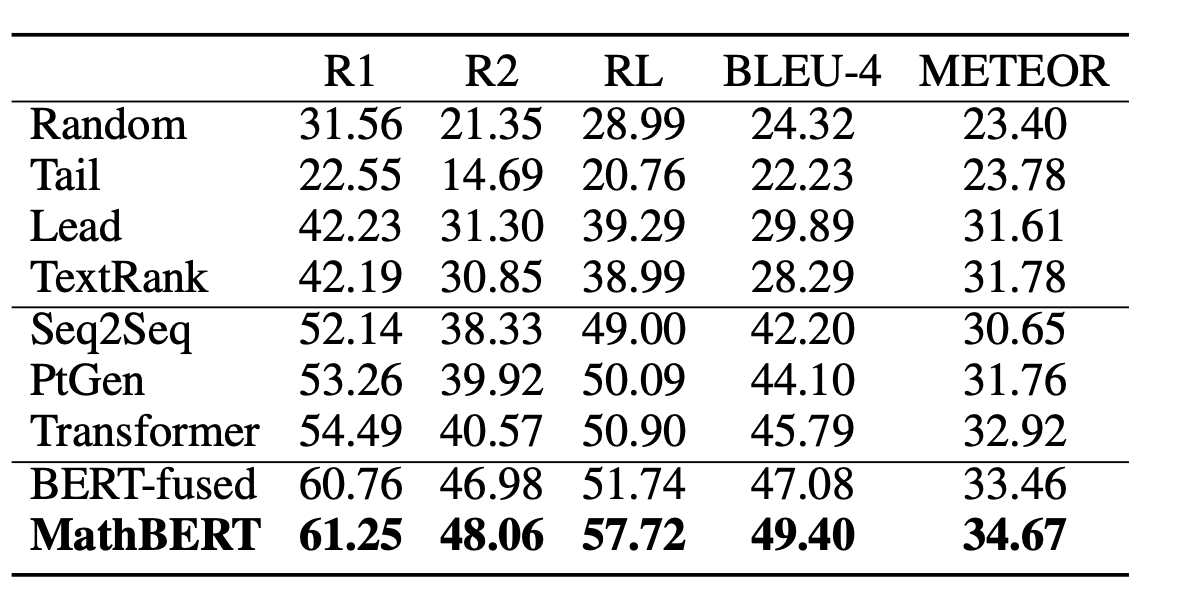
Untitled

Formula headline generation result

배경

수식이 들어가 있는 문서는 context랑 수식이 함꼐 있고, 수식의 한 요소와 context의 부분이 매핑이 됨. 수식 보여주고, 이 수식에서 E는 ~~~다. 이런식으로.

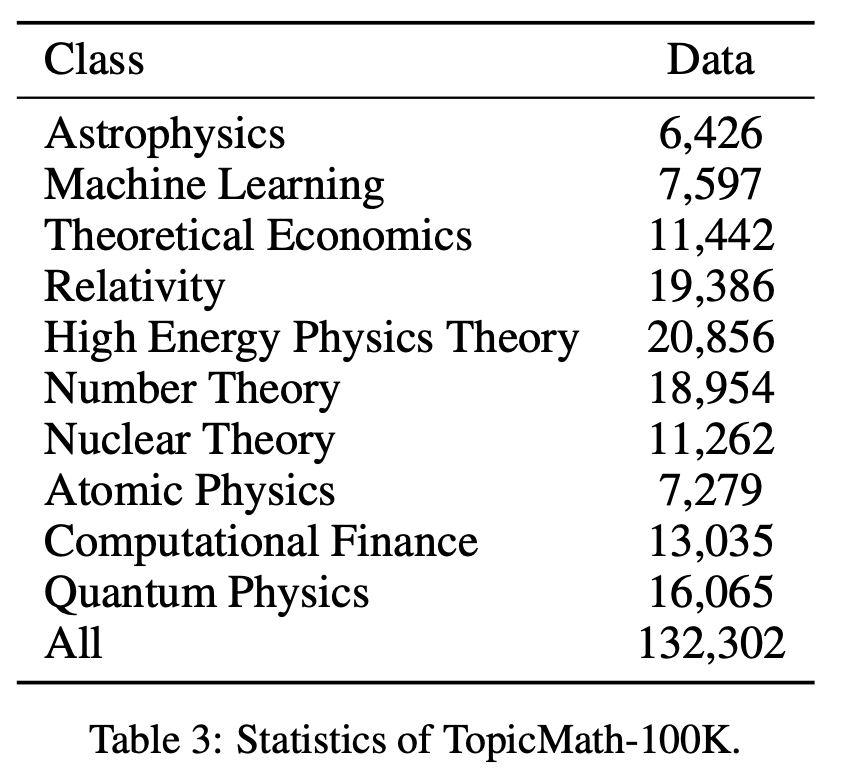
Untitled

데이터

Untitled

axiv에서 긁어왔다고 함니다. 가지고 온 문서 종류 보여줌.

모델

  1. 일단 기존의 사전학습된 버트를 가지고 와서 추가적이 사전학습을 시도
  2. 세가지 목적을 달성하고자 했음

2.1 수학 도메인에서 text context을 이해하자! → 기존 버트의 MLM에 해당(MLM)

2.2 수식과 context의 관계를 학습하자! → 기존 버트의 next sentence prediction에 해당(CCP)

2.3 인간이 사용하는 수식의 구조를 이해하자! → 이 논문에서 새로 제안한 방법. 구조에 대한 MLM이라고 볼 수 있음(MSP)

  • 이거 하려고 모델에 입력을 다음과 같이 설정함
<CLS> latex <SEP> context <SEP> OPT<EOS>

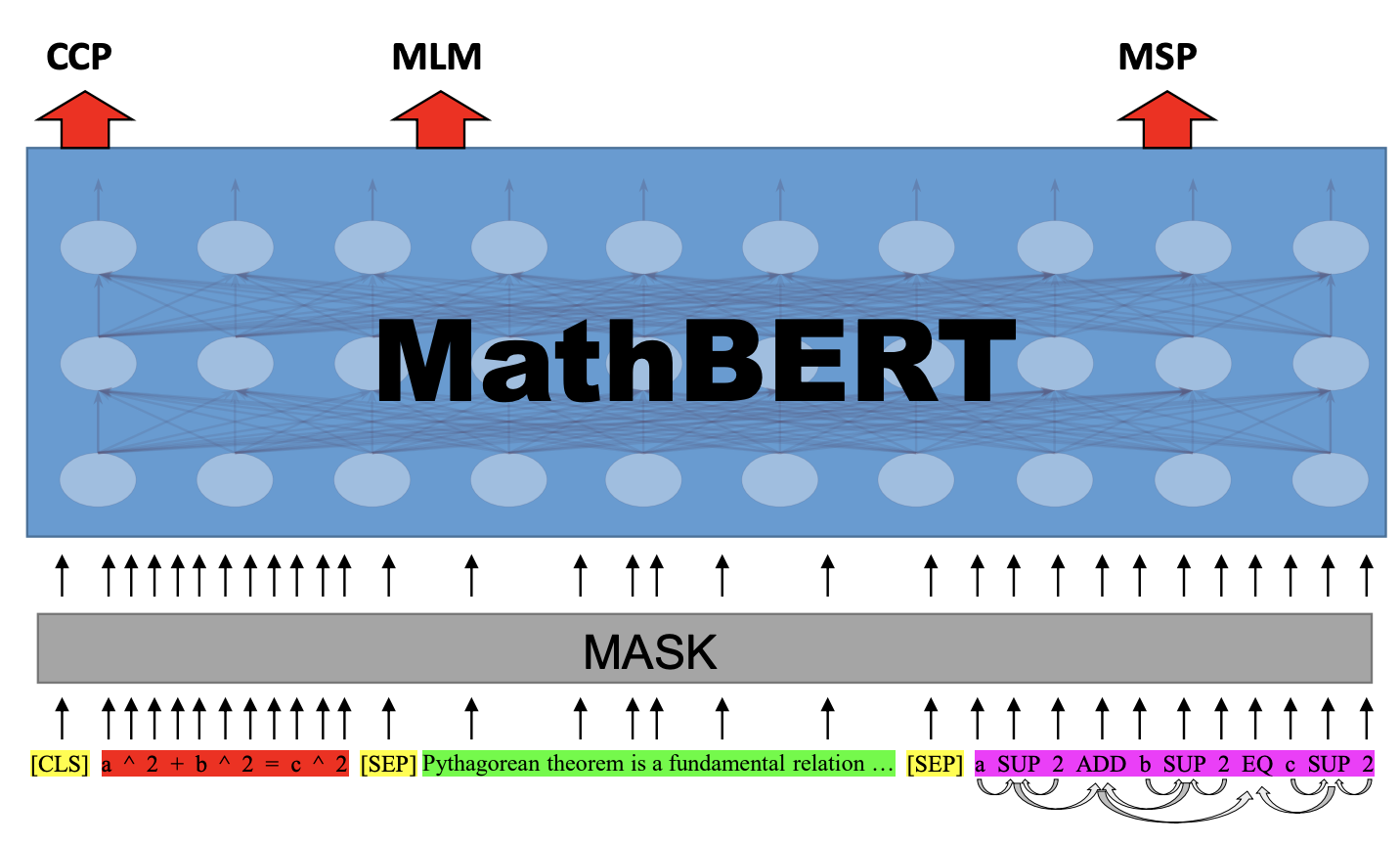
Untitled

  • 여기서 OPT는 operator tree의 약자로, 수식의 구조화된 표현임. mathML이 여기에 해당? 수식을 latex는 인간이 사용하는 표현이라면, OPT는 그래프 형태로 수식을 표현했음. 인접한 기호나 operator가 edge으로 연결됨.
  • 근데 수식에 대해서 새로운 attention mechanism을 제안함. OPT 그래프로 표현되어 있을 때 인접하지 않은 노드들에는 그냥 관심을 끄도록, 인접한 노드가 아니면 attention mask을 걸어줬음.

Untitled

3 사전 학습 task

3.1 수학 도메인에서 text context을 이해하자! → 기존 버트의 MLM에 해당

  • latex와 context 토큰들에서 15% 뽑아서, 80%는 마스킹, 10%는 랜덤한 문자로 바꿈, 10%는 그래도 둠. 마스킹 한 부분을 예측하게 함. cross entropy으로 학습.

3.2 수식과 context의 관계를 학습하자! → 기존 버트의 next sentence prediction에 해당

  • latex와 conetxt가 원래 데이터에서 함께 들어갈텐데, 여기에서 context을 랜덤한 다른 context으로 바꿈. 그리고 binary classification으로 이 수식 다음에 오는 context가 잘 연결된 것이 맞는지 학습.

3.3 인간이 사용하는 수식의 구조를 이해하자! → 이 논문에서 새로 제안한 방법. 구조에 대한 MLM이라고 볼 수 있음

  • OPT는 그래프로 표현 됨. 이 그래프의 노드들에서 15%을 뽑아서 연결된 edge들을 모두 끊음. 그리고 이 노드가 어떤 노드들이랑 실제 egde을 가지는지 학습하게 함! loss으로 cross entropy 사용. 주어진 노드 n_j에서 n_i 노드로 연결된다고 예측하면, 실제 맞는지 여부가 1 혹은 0과의 차이가 loss가 됨. 이 값이 back propagatoin에 사용되어서 학습 함.
  • 최종 loss는 위 3가지 loss의 합이 된다.
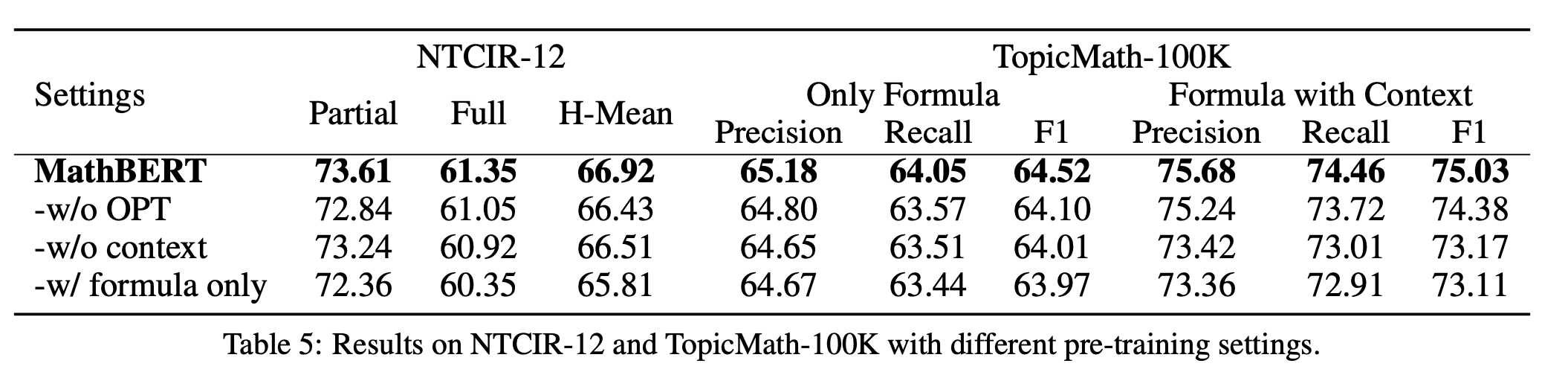
  • 다양한 실험 결과

Untitled

수식 표현

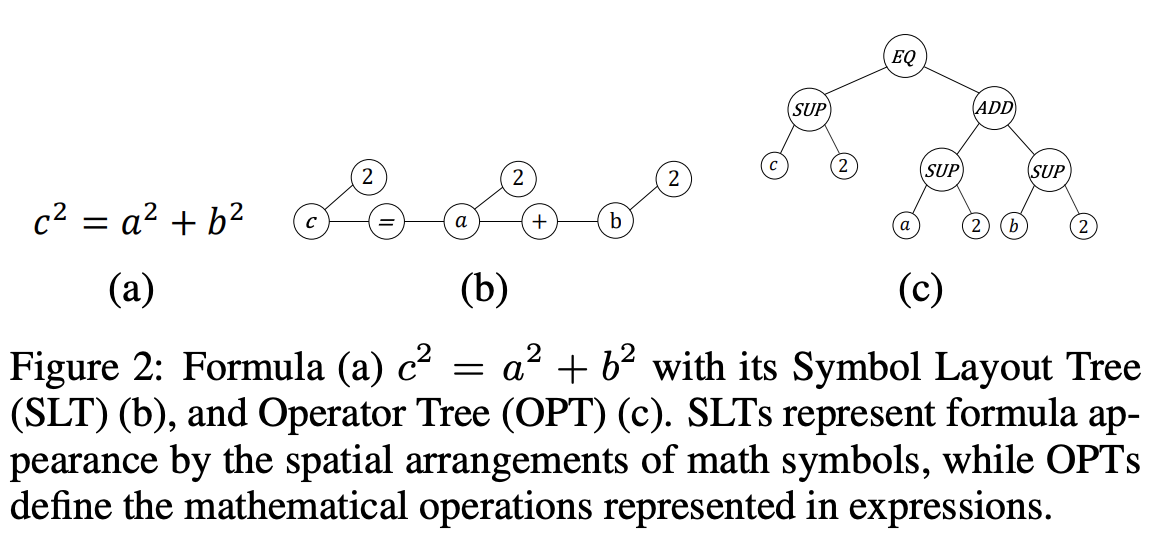
이 사람들이 수식을 모델에 학습 시키는 것에 관심을 가졌기 때문에 수식을 어떻게 표현할까 고민을 많이 했음. syntax한 표현이 있는 latex을 넣고, 여기에 구조적인 의미를 더 주고싶어했음. 그래서 OPT을 넣은건데, 사실 OPT을 사용하기 전에 다른 구조적인 표현으로 symbol layout tree(SLT)도 고민했음. 이 두개 중에 몰 쓸까 고민했는데, 결국 SLT안스고 OPT을 쓴 이유는…. SLT에서 얻고자 했던 표현이 이미 latex에 있다고 판단했다고 함.

Untitled

특이사항 및 개인적 감상평

  • 중국 mathBERT는 코드도 공개하지 않았음
  • 그리고 아이디어가 쫌 신선했음. OPT으로 수식 구조를 넣어서 이 구조에 맞게 masking 하는거랑, OPT 학습할 때 수식 구조 attention을 따로 만든거?
  • 만약 구현한다면?
  • OPT을 어떻게 만들지? mathML을 그대로 사용하는 것도 방법일 수 있음. 근데 mathML은 이 논문에서 표현하는 OPT랑 표현이 정확히 일치하지는 않음. 이 논문에서는 latex을 OPT으로 translate 했다고만 표현하던데, 이걸 해주는 라이브러리를 못찾았음. 그래서 이걸 따로 구현한다면, 수식을 인접한 노드끼리 연결하는 그래프를 구현해야 함.
  • OPT attention mask는? 인접하지 않은 노드들에 대해서
  • 노드 * 노드의 array 기반 그래프 표현이라고 하면… 연결되어 있지 않으면 모두 -inf 값을 주면 되겠다! attention을 직접 수행하는 부분은… 노드 * 노드의 attention으로 표기. 기존 attention의 방법 역시 len * len의 정방 행렬에서 수행되니까 동일하게 적용하면 될듯!

Comments

You May Also Enjoy