DPO review
DPO
한줄 요약: HFRL할때 reward 모델 재끼고 선호 데이터셋만 있으면 바로 학습 가능.
Direct Preference Optimization: Your Language Model is Secretly a Reward Model
TDLR;
- instructGPT에서는 PPO을 사용해서 align했다. 근데 reward 모델을 추가로 학습시켜야 했음.
- 이 논문에서는 중간 단계의 reward 모델을 생략함.
- 그리고 그게 어떻게 가능한지 이론적으로도 보인다.
3. preliminaries: InstructGPT에서는 어떻게 했는지 복습하기
- SFT
- downstream task에 대한 학습
- Reward Modeling Phase
- SFT 모델로 여러가지 output을 만든다.
- 라벨러에게 선호하는 대답을 고르게 한다.
- 사람의 선호를 반영하는 latent reward model r*을 가정함.
- 이 선호를 모방하기 위한 아키텍처가 몇개 있는데… binary 선호라면 Bradley-Terry Model을, 선호 체계가 여러개라면 Plackett-Luce ranking model이 유명하다.
- BT model은 사람의 preference distsribution을 이렇게 정의함.
-
식 1: preference probability
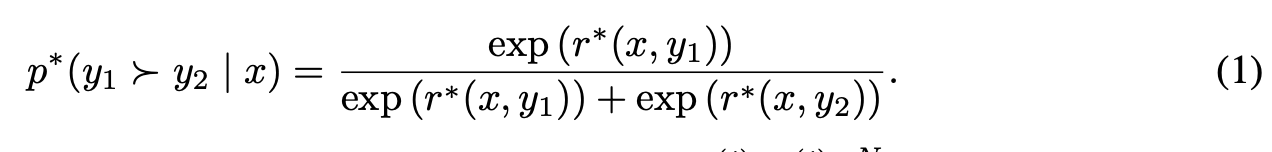
- example 2개가 있을 때 y1을 y2 보다 사람이 더 선호할 확률은 각 y1, y2에 대한 latent reward model이 정한 점수의 softmax이다. 이 확률도 latent에서 나온 가상의 혹은 맞춰야 하는 확률분포이다. 이 확률분포가 모방해야 하는 r에 연동되어 있음. 그래서 r을 잘 모방하면 이 선호확률도 예측할 수 있다.
- 이 확률분포에서 sampling을 몇개 해서 라벨링한 결과가 나왔다고 보는 것. 이 확률에서 나온 데이터를 통해 r*을 모방한 r pi을 만들고자 한다. 따라서 maxmum likelihood을 통해서 예측한다. 기대정보량이 극대화하도록 함. 따라서 minimize negative log likelihood.
- 따라서 다음의 objective을 minimize하면 된다.
-
식2: reward network 학습 목적 함수
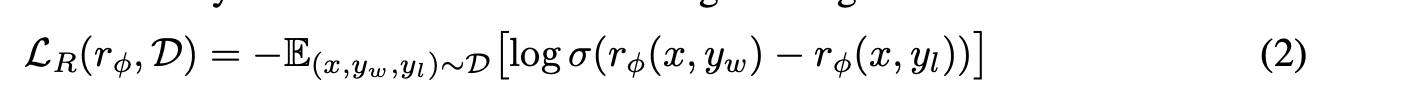
- 좋은 output이 안좋은 ouptut 보다 크면 값이 커진다. 확률 값이 커진다. GT는 1이다. 1과 실제 확률 값의 분포가 클수록 cross entropy는 올라가고 loss 값은 커진다.
- r pi는 SFT로부터 initiallized 되고 r_pi network을 학습하면 된다. r pi는 마지막에 scalar layer을 하나 추가하면 됨.
- RL Phase
- 위에서 학습한 reward 모델로 언어모델이 뱉은 결과에 피드백을 준다. 지금 낸 output은 4점, 그 다음에 낸건 8점 …
- 이 피드백을 통해서 언어모델을 다시 학습한다. 점수를 더 높은 것을 내도록!
- 우연히? 뱉은 어떤 output의 rewward을 계산해본다. 만약 이 reward가 크다면, 앞으로 더 자주 나와야 한다! 따라서 parameter을 이동시킬 때 더 많이 이동시켜야 해서 argmax을 한다!
- 근데 이때 어떤 한 값의 reward가 잘 나오면 그 값만 나오게 될수 있음. 그래서 reference 모델과 분포 차이 만큼 조금 깎아주면서 학습한다.
-
식3: policy network 목적 함수
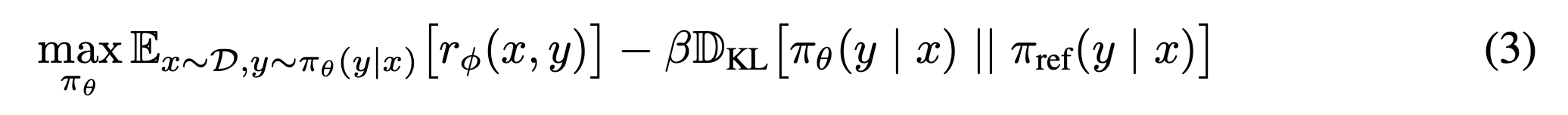
- PPO을 통해서 학습 함.
- 이 식은 PPO 논문에서 다음 식과 같은 의미
- instructGPT 논문: https://arxiv.org/pdf/1707.06347.pdf
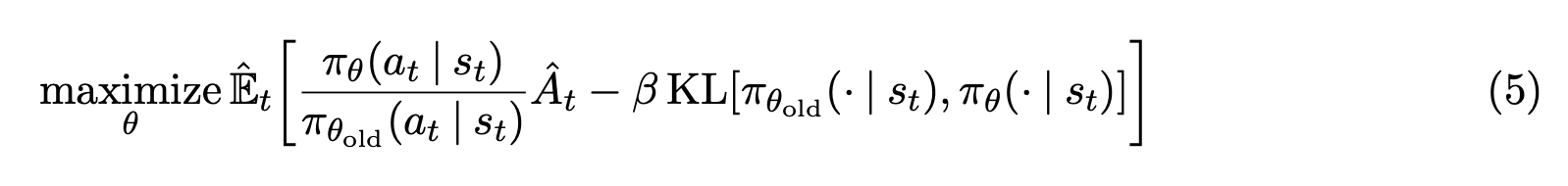
- PPO으로 학습한다 = 너무 과도하지 않게 reward을 계산한다.
- PPO 논문:
- PPO 자세한 설명 문서:
- 모델의 결과에 reward 모델로 reward을 계산한다.
- V target 값은 일정 앞 토큰들 + 그 다음 토큰들의 reward을 state value network으로 예측
- stage value network을 V Target 값으로 학습시킴(loss 1)
- (state value network - V target): 평균 보다 sampling 된 것이 더 reward가 좋다면 더 자주 나오도록 학습함. 그래서 Clipping을 걸어준다. (loss 2)
-
explore 하도록 Entropy 값을 loss에 추가함 (loss 3)
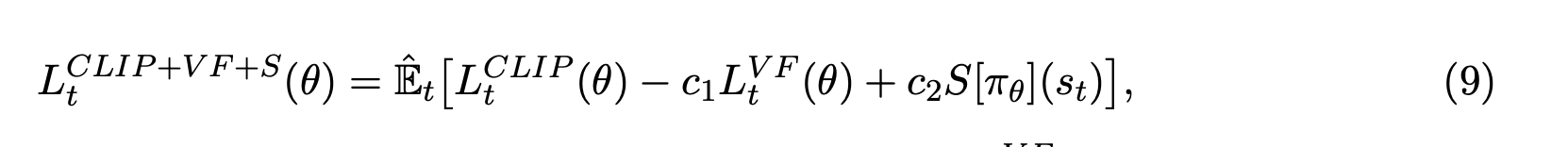
-
너무 과도하게 업데이트하지 않도록 clipping
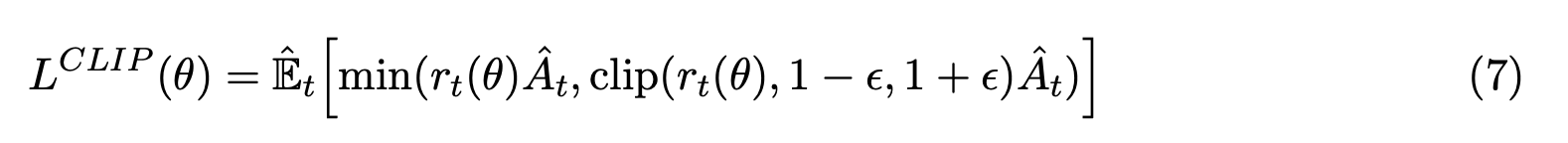
- 근데 대신 이렇게 쓸수도 있다. 같은 직관이고 정확히 같지는 않지만 같은 역할을 함. 이게 사실 instructGPT에 나온 수식. 사실 이렇게 구하나 cliping을 구하나 역할이 같다.
- 평균 보다 sampling 된 것이 더 reward가 좋다면 더 자주 나오도록 학습함(A_t)
- 너무 과도하게 update가 되지 않도록, 지난번 확률 값으로 나눠서 보정을 해준다.
- reference에서 너무 멀어지지 않도록 값을 좀 깎는다.
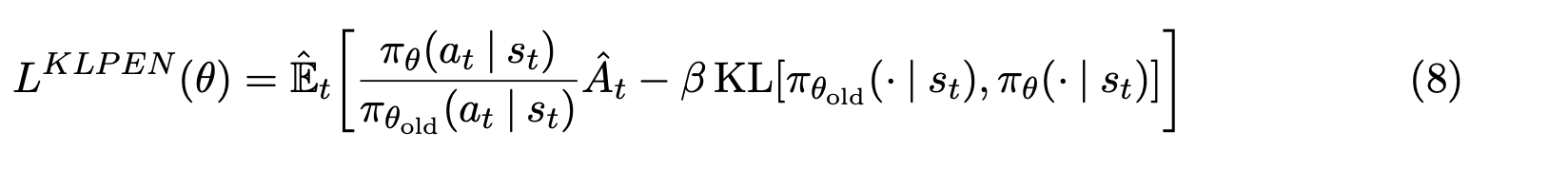
4. Direct Preference Optimization
- Derive DPO
- 식 3(식3: policy network 목적 함수)에서 policy을 학습 함. DPO도 같은 것을 목표로 함. 그래서 식 3에서부터 시작. 식 3에서 appendix A.1을 거치면 다음과 같이 됨. 식 3을 최적화하면 나오는 optimal solution에서 최적 policy network 식 4을 얻음.
- 식4: optimal policy network.
- 직관
- policy 함수를 최적화할때
- 최적화 되기 위한 조건이 바로 식 4이다.
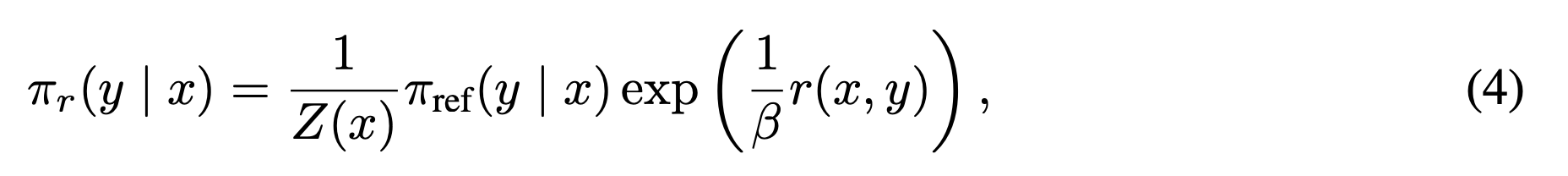
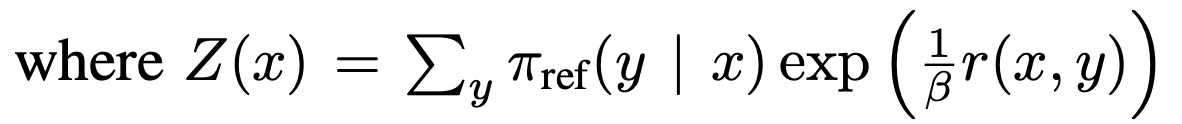
-
Appendix A.1
식3 = 식 11

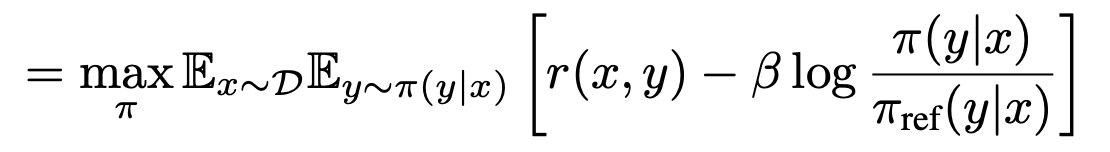
reward는 사실상 상수이다. 학습에 사용하지 않음. 저 크기 많은 policy에 업데이트 함. 방향에서는 변화가 없음. 1 / beta을 곱한다. -1을 곱해서 max 에서 min으로 바꿈.
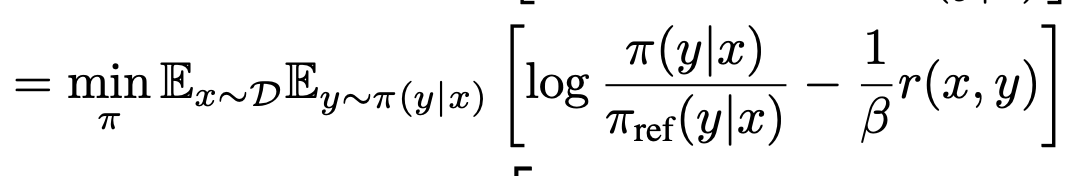
간결하게 하기 위해 치환 Z
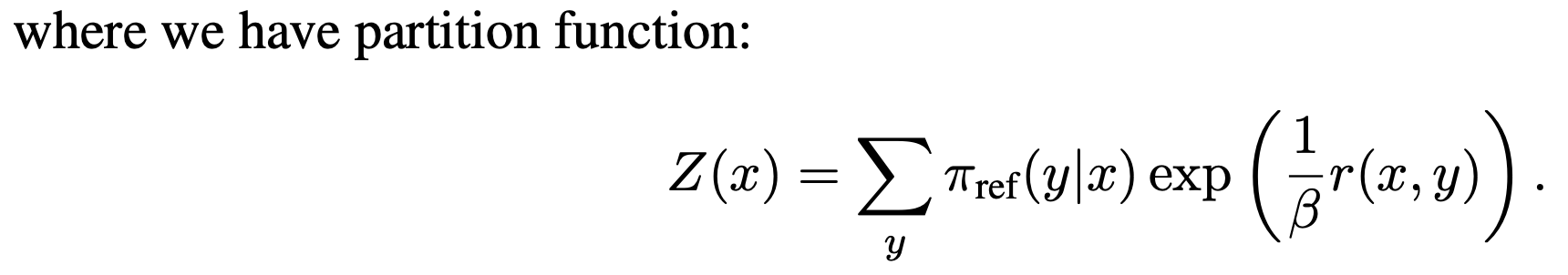
Z 대입
- 앞 항:
- Z 안의 $\sum \pi_{ref}=1.$
- $Z(x) = \exp (\frac{1}{\beta}r(x,y))$
- exp 항은 분자 분모 약분으로 1.
- 원래 식의 $\pi_{ref}$만 남는다.
- 뒤 항:
- $log Z(x) = log \exp (\frac{1}{\beta}r(x,y)) = \frac{1}{\beta}r(x,y)$
- Z 안의 $\sum \pi_{ref}=1.$
- $\log \exp = 1$으로 원래 식의 $\frac 1 \beta r(x, y)$만 남는다.
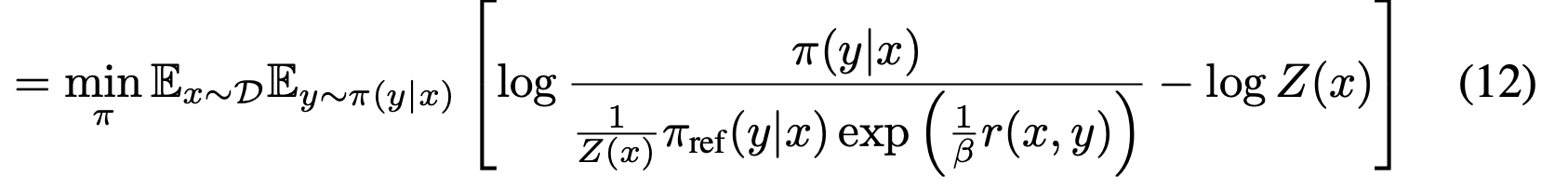
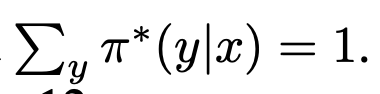
-
partition function을 변수로 치환함
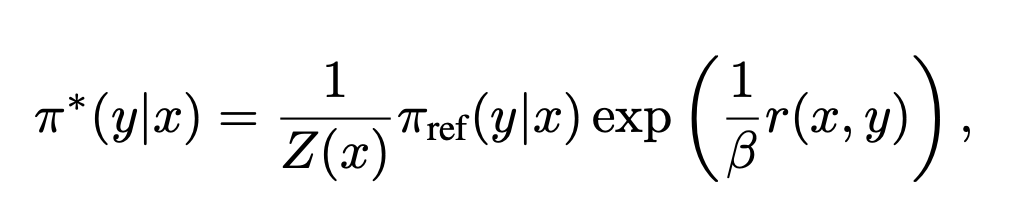
-
다시 식 12에 넣으면
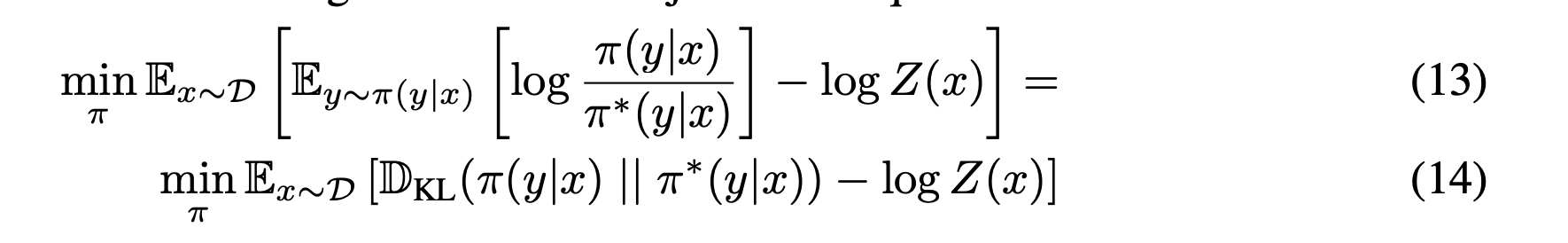
- optmize하는 pi가 Z(x)에 대해 없어서 KL div term으로 optimize 한다.
- 이때 Gibbs inequaility: KL div = 0 where two distribution identitcal. 따라서
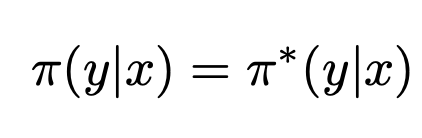
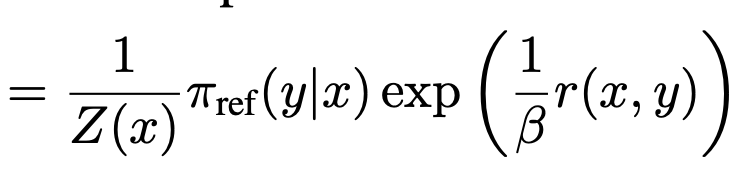
가 되도록 parameter이 이동하면 최적화된다.
- 앞 항:
-
discussion
어차피 ref에 도달해야… 변형 없이 처음부터…
reward으로 r(x,y)라서 pi에 상관 없음…
optimize도 결국 ref에 비슷해야 최적화….
- 직관
- 근데 여기에 아직 reward 함수가 남아있음. 여전히 instructGPT 와 같이 선호 데이터 MLE(maximum likelihood estimation)으로 구해줘야 함. 여전히 비싸다! 없앨 수 없을까?
- 식 4에log 씌우고 계산을 좀 하면 다음과 같이 됨. 즉 optimal reward 함수를 구하는 것 = policy network을 구하는것과 동일해진다!
-
식5: optimal reward network 최적화 = optimal policy network
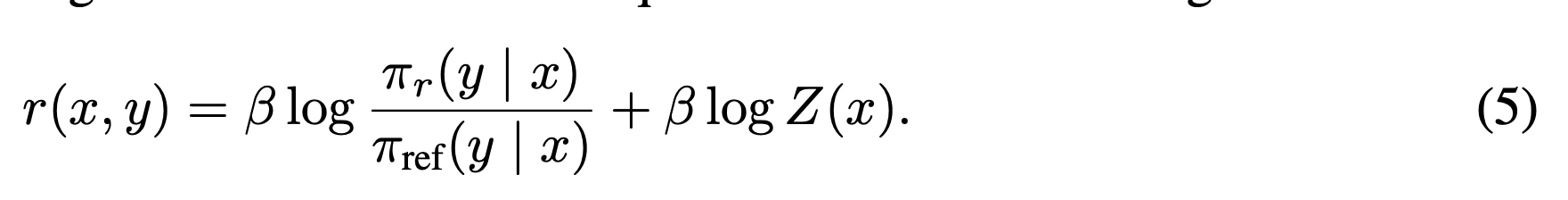
- BT 모델에서 구하는 선호 확률은 reward 모델을 sigmoid 한 것. 식 1(식 1: preference probability)에 식 5를 그대로 대입하면 (혹은 appendix A2) 식6.
-
식6: 선호 확률을 optimal reward 대신에 optimal policy network으로 표현함.
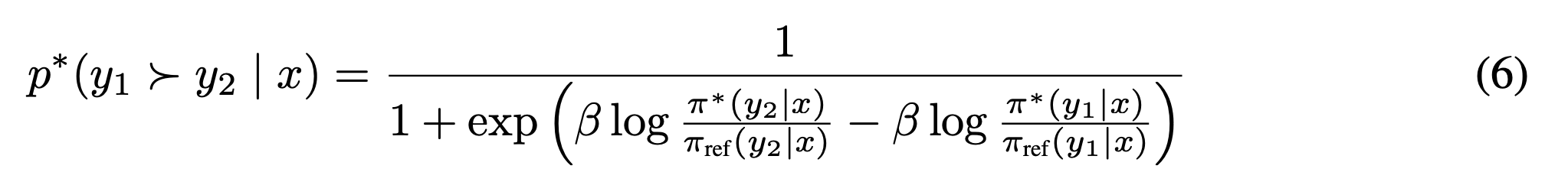
- 따라서 이제 optimal policy network을 구하면 사람의 선호 확률을 구할 수 있다. = optimal reward을 구하면 optimal policy network을 알 수 있다. 둘중 하나만 구하면 됨.
- 근데 여기서 policy network을 최적화할 때 reward model을 최적화하듯이 objective을 정의함. 조금 이상하긴한데 수학적으로 동일하다는 것을 이후에 증명함.
- 식 2(식2: reward network 학습 목적 함수)는 reward을 최적화하는 식임. 여기에 식 5는 reward을 policy network으로 표현함. 그래서 식2에 식 5을 그대로 대입하고 조금 정리하면
-
식7: reward network 최적화(식2)를 policy network(식5)으로 표현함. (혹은 A3)

5 Theoretical Analysis of DPO
- DPO는 reward 모델을 생략함.
- optimal policy을 구하지만 reward 처럼 loss 계산을 한다. (식7)
- 그래서 어… 쫌 그래… 이거 진짜 이론적으로 돼? 하는 질문에 대답하는 단락
- eq5에서 reward function을 정의함.
- eq5 → partition function을 생략하면서 → eq6 에서 두 generation에 대해 선호 확률을 계산함
- reward 모델 없이 선호 확률을 계산하게 됨. 따라서 eq7에서 policy update loss에 선호확률을 사용함.
- 근데 원래는 eq2 처럼 reward 모델 자체의 loss을 경감시켜서 선호 확률을 학습해야 함. 이게 과연 같은 것인가?!를 이론적으로 증명하기
- Deffinition
- 두 reawrd functions는 equivalent하다. iff 한 reward r(x,y) - 다른 reward r(x,y) = f(x)
- Lemma1: same eq 에 속하는 모든 reward 네트워크는 동일한 선호 분포를 가진다
- Under Plackett-Luce, 특히 Bradley Terry, same class에 속한 두 reward functions는 동일한 선호 분포를 가진다.
- 직관: 입력 x에 대한 모델 랜덤 변수 함수 y에서, 여러 y 값의 선호 확률에 대하여, 입력 x에 대한 함수의 선형 변환이 있어도(=같은 class에 속함) 선호 확률은 변화가 없다.
-
증명: 2,3 줄은 1번 줄에 $\frac{exp(f(x))}{exp(f(x))}$을 곱하고 summation 안으로 분배법칙을 씀.

- Lemma1으로 인해 eq2에서 reward loss을 감소시켜서 reward model을 학습 시킬 때 identifiability 제약이 필요함.
- Under Plackett-Luce, 특히 Bradley Terry, same class에 속한 두 reward functions는 동일한 선호 분포를 가진다.
- Lemma2: same eq 에 속하는 각 reward에 대한 optimal policy network는 사실 같다.
- same class에 속한 두 reward functions는 RL 제약 안에서 동일한 optimal policy을 가진다.
- 직관:
- same class에 속한 reward 함수는 선형변환 됨.
- 선형변환된 reward의 optimal policy network는 기존 reward으로 표현할 수 있음.
- 약분 됨.
- 기존 reward network의 optimal policy network와 같아짐.
- 증명
- 식 4: optimal policy network에서 시작.
- same equivalance class에 속한 reward 들은 선형변환 될 수 있음.
- 약분 됨.
- reward에서 선형변환된 다른 reward의 optimal policy network와 같아짐.

- lemma2으로 인해 어떤 reward의 optimal policy을 알고 싶을 때 동일 class의 임의의 reward function의 optimal policy을 구할 수도 있음.
- discussion:
- 식 4는 어떤 reward을 최적화할 때 도출되는 파생물. 파생물로써 optimal policy network.
- 연결된 lemma2의 의미: 각 reward을 최적화하면 나오는 policy network들이 모두 동일하다.
- Theorem: same eq에 속하는 모든 reward는 사실 어떤 optimal policy network으로 표현될 수 있다.
-
Llackett-Luce 군에 속하는 모든 reward 함수는 policy network와 reference policy network으로 표현할 수 있음. 완전히 동일한 의미를 가짐.
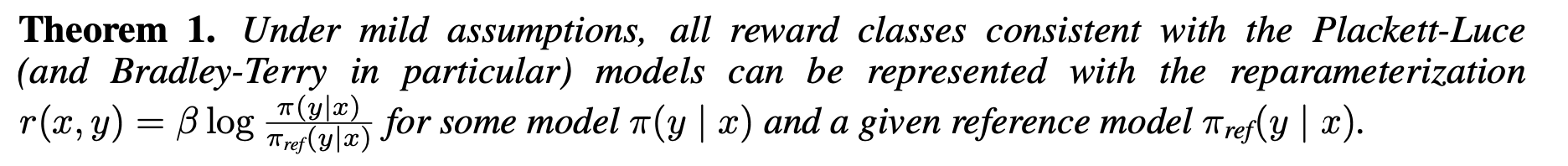
-
reward 함수를 reparameterize 하는 사상함수 f를 정의
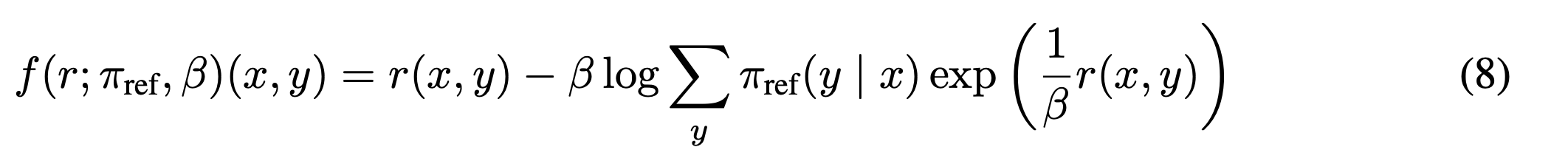
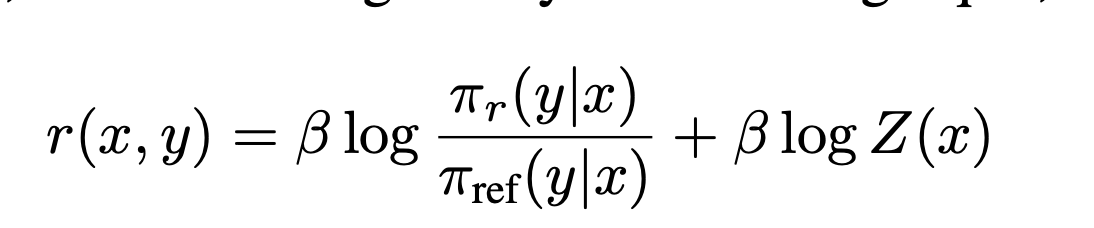
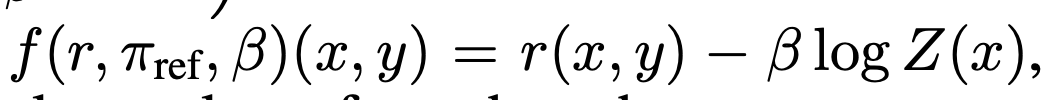
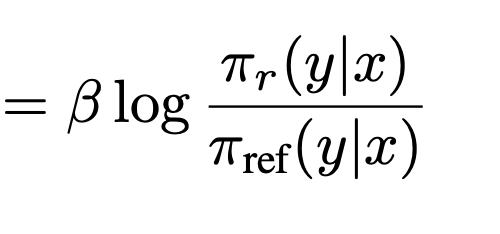
- 그냥 x에 대해 이동시킴
- 근데 definition에 의해서 이동시켜도 equivalent하다. 따라서 이동시켜도 optimal policy network을 가진다(lemma2).
- (약간 더 엄밀한?) 증명: reward 함수 $r_1$은 $r_1$말고 다른 어떤 reward $r_2$에 대한 optimal policy network으로 표현될 수 있다($r_1$에서 $Z(x)$ 만큼 linear 하게 선형변환한 $r_2)$
- 어떤 reward $r$이 있고 이 reward는 $\pi_r$에 대한 term과 $r$에 종속된 $Z(x)$ 만큼의 이동 값으로 표현될 수 있음(식5: optimal policy network으로 reward을 표현. ← 식 4: reward을 최적화할 때 optimal policy network 가 파생 됨)
-
이 optimal policy network는 reward에서 $\beta \log Z(x)$만큼 떨어진 다른 reward을 표현할 수 있다.

- discussion: lemma2와 차이점
- lemma2: same equivalance class에 속하는 두 reward들은 (혹은 두개씩 따왔을 모든 pair들은) 최적화하면 동일한 optimal policy network을 가진다.
- theorem: same equivalance class에 속하는 reward들을 그 reward에만 의존하는 $Z(x)$만큼 선형변환과 함께 표현하는 optimal policy network는 다른 reward을 표현할 수 있다.
-
- 따라서 reward 함수의 loss을 감소시키는 것은 policy network의 loss을 감소시키는 것과 동일하다. 따라서 식 7에서 reward model을 최적화하는 역할로 policy network을 최적화하는 것이 정당화된다.
더 엄밀하게 살펴보기. proposition: 사실 equivalent class에 있는 모든 reward는 단 하나만 존재한다. 그리고 각 reward에 연결되어 있는 optimal policy network도 하나이기 때문에 equivalant class에는 단 하나의 optimal policy network만 가지고 있다.

- 따라서 reward 함수의 loss을 감소시키는 것은 policy network의 loss을 감소시키는 것과 동일하다. 따라서 식 7에서 reward model을 최적화하는 역할로 policy network을 최적화하는 것이 정당화된다.
- 증명:
- contradictory premise: $r_1$에 $f(x)$ 만큼 이동하면 $r_2$로 정의하자. $f(x)=0$이 아닌 이상 $r_1$과 $r_2$는 다르다.
- contradictory premise: 그리고 $r_1$을 표현할 수 있는 optimal policy $\pi_1$와 $r_2$을 표현할 . 수있는 optimal policy $\pi_2$가 다르다고 하자. ($\pi_1 \neq \pi_2)$
- r1은 또 다른 reward을 선형변환과 함께 표현하는 policy network으로 표현 됨.
- r2도 또 다른 reward을 선형변환과 함께 표현하는 policy network으로 표현 됨.
- 근데 전개하면 $f(x)=0$이 되어야 함. 따라서 $r_1 = r_2$이고, $\pi_1 = \pi_2$이다. premise가 모순 됨.
- 따라서 same equivalance class는 단 하나의 reward와 optimal policy network을 가진다.

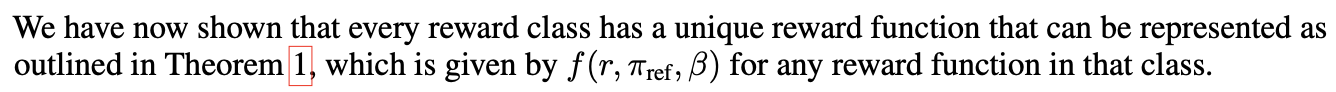

Comments