Transformer 의문점 정리

Transformer 의문점 정리

궁금한 내용

1. pad mask을 구현할 때, 실제로 어떻게 masking이 되는지? → 해결!
2. auto-regressive한 디코더를 만들기 위해서 masked self attention을 함. 뒤의 내용을 모르는 상태에서 예측하는 훈련임. 근데 실제 학습할 때는 이걸 동시에 triangular mask으로 수행함. 동시에 하는데 이렇게 굳이학습할 필요가 있나? 여기에 대해서 구체적인 흐름을 살펴보고 직관적인 설명을 달아보고자 함
3. 논문에서와 구현할 때 multi head attention의 의미가 조금 다른 것 같음. 논문에서는 h_model을 다른 멀티 헤드로 보낼 때 linear layer 넣어서 축소해서 여러 head에 넣는다. 구현에서는 linear에 넣을 때 d_model로 들어가서 d_model으로 나옴. 그 다음에 d_model을 쪼개서 sub vectorspace으로 나눈 다음에 multihead attention에 각각 집어넣음.

1. pad mask 구현

a. 알고 있었던 내용

transformer에 마스크가 두 종류가 있음. pad mask와 triangular mask. pad mask는 input text에서 max_seq_length보다 짧으면 그 부분을 pad token으로 채움. decoder의 경우 디코더 train data의 pad mask와 함께 masked self attention에 사용할 mask가 하나 더 필요함. (seq_len, seq_len) 크기의 triangular mask가 들어감.

• 인코더에서 mask

Q, K, V의 차원은 (len_seq, h_dim)이다.

attention 가중치 Q * K.T 는 (len_seq, len_seq)가 된다

att_w = Q * K.T

여기서 mask 추가요! 그리고 softmax 걸어서 토큰 별 가중치 구하고, V와 내적해서 연관있는 토큰끼리 가중 sum을 한 hidden representation을 얻는다.

masked_att_w = att_w.masked_fill(pad_mask == 0, float('-inf') # mask = 0 인 위치에 -inf을 넣는다.
weight_att_w = torch.nn.functional.softmax(masked_att_w) # (seq_len, seq_len)
weight_v = weight_att_w @ V #(seq_len, d_model)

Q와 K는 사실 동일한 텐서이다. 그리고 내적할 때 T는 transpose 되어야 내적이 가능. 근데 어차피 두 텐서가 같은 텐서이니까, mask도 transpose 되어야 한다. Q와 K에 각각 있는 pad들이 인코더에서 attention을 구할 때 모두 무시되어야 함. 그뿐 아니라 디코더에서도, 그리고 디코더를 지나서 train 함수에서 loss을 구할때에도 padding이 무시되어야 함… 그래서 masking을 Q와 K을 따라 둘다 구해는 구현체는 납득이 간다.

# given tokenized,indexed, and containig special token, data
# given pad_idx <- padding index
def create_mask(data, pad_idx):
	pad_mask = torch.tensor( data != pad_idx )
	pad_mask = pad_mask & pad_mask.T

	return pad_mask

b. 궁금했던 부분: Q와 K에 둘다 padding이 있는데 한 방향만 masking을 적용해도 괜찮을까?

그런데 사실 아주 많은 구현체들에서 이렇게 않하고 그냥 하나만 만들어둔다… 이렇게 하면 어떻게 K의 transpose에 그래도 남아있는 pad을 마스킹할 수 있는건지?

# given tokenized and indexed sentence, tok_sen
# given pad_idx <- padding index
pad_mask = torch.tensor( masktok_sen != pad_idx )

c. 공부한 부분:

• 결론 먼저 말하자면, 괜찮다. 왜? 일단 한 방향으로 패딩을 하면 분명이 다른 방향의 패딩은 남는데, loss을 구할 때 Cross Entropy을 사용하고 이때 ignore_index으로 pad가 ground truth인 토큰을 학습하지 않음.
• 차근 차근 알아보기

가정: max_seq_len = 5이고, hidden_dimension = 3이다. 그리고 아래 그림에서는 multihead attention을 사용하지 않는 상황처럼 묘사했다. hidden_dim이 multihead attention의 dimension으로 쪼개진 상황일 것이다.

1. 각 토큰이 인코더로 들어와서 linear layer을 거쳐, Q, K, V으로 변환된 상태이다. masking 텐서는 [1,1,1,1,0]의 형태를 가질 것이다.

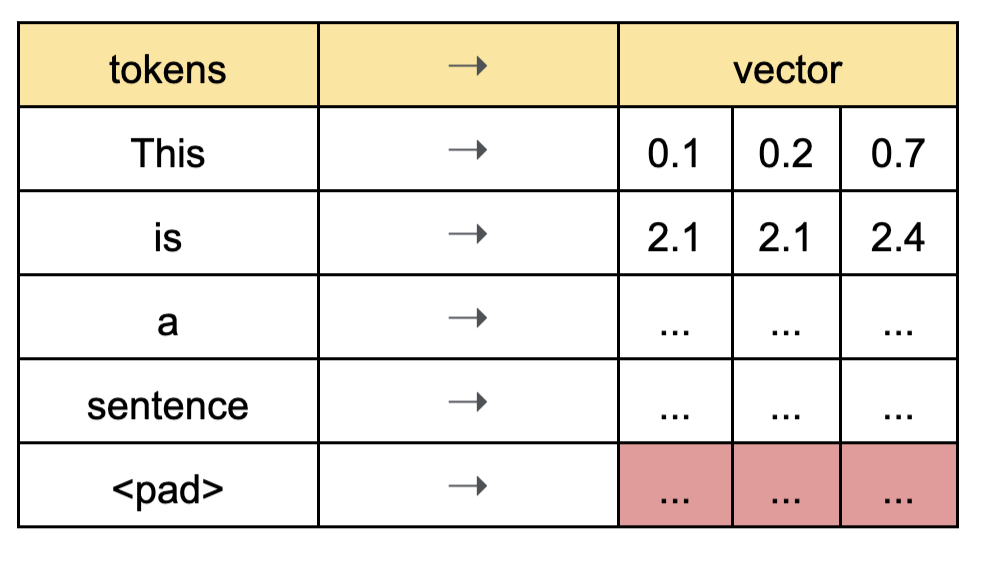Q

1. K도 Q와 동일한 텐서이고 내적을 위해서 transpose만 하면 이런 모양이 된다. 마스킹이 되어야 하는 부분을 빨강과 파랑으로 표현.

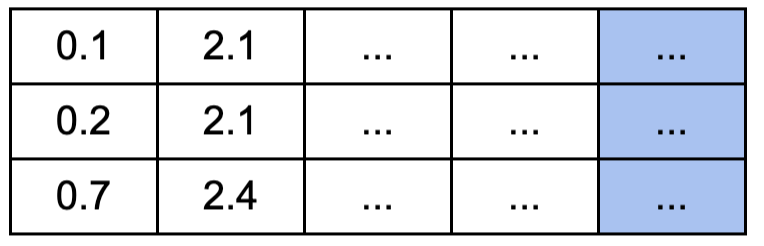
K.T

1. 두개를 내적.

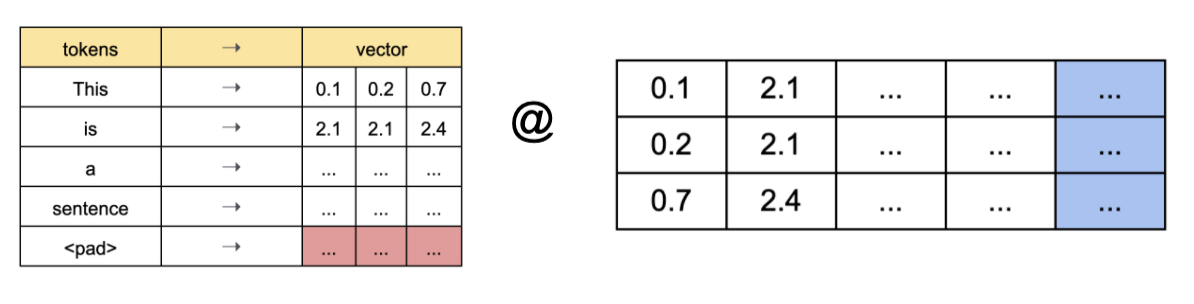
3-1. K의 pad와 내적된 부분을 파랑색으로 그대로 표현했고, Q의 pad와 내적된 부분을 빨강으로 표현했다. 사실 이 두 부분 모두 무시되어야 할 부분이다. 각 row의 직관적인 의미는 i번째 row에 해당하는 토큰이 다른 토큰들에 가지는 유사도라고 볼수 있다. 1번째 column은 1번째 token과 유사도, 2번째 column은 2번째 token과 유사도,… 여기에 softmax만 넣으면 각 토큰이 다른 토큰들에 미치는 가중치라고 볼 수 있다. 파랑색 부분은 다른 토큰들이 pad와의 유사도를 의미한다. 빨강 부분은 pad가 다른 토큰들과의 유사도.

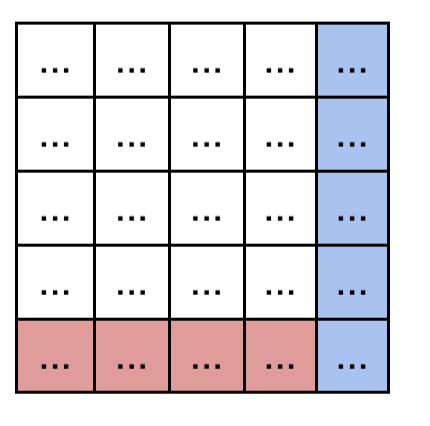
Q @ K.T

1. 여기에 Q의 pad mask을 적용한다. 이때 pad mask의 차원은 (B, len)인데, 현재 내적된내적된 행렬의 차원은 (B, len, len)이기 때문에 중간에 unsqueeze(1)으로 (B, 1, len)으로 만들어주고, masking 해주는 함수 masked_fill을 호출한다. 이 함수는 broadcastable 해서 병렬적으로 각 row에 동일하게 적용 됨. 따라서 파랑색 부분이 masking 된다.

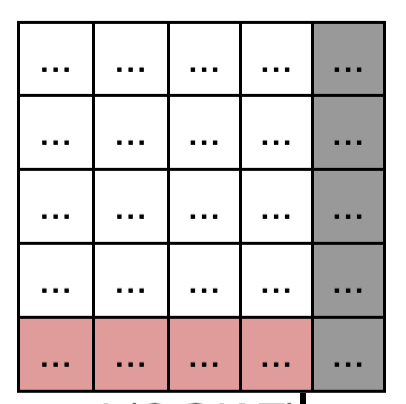
1. 이 상태에서 softmax에 넣으면 masking된 부분이 0이 됨! 각 row는 개별 토큰이 다른 토큰들과의 유사성에 대한 가중치가 되었다.

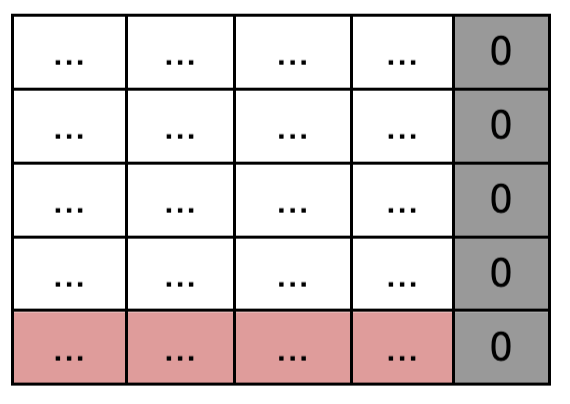
softmax( mask(Q@K.T) )

1. v는 Q,K와 동일한 행렬이다. 패딩 영역을 녹색으로 표현

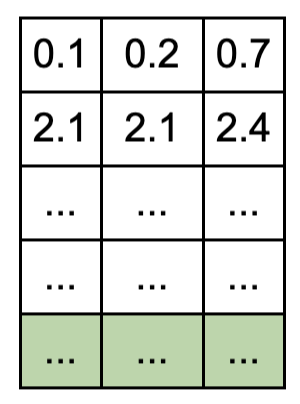
v

1. v와 다시 내적을 한다. 하나의 분홍색 row가 v의 각 column에 내적된다. 분홍색 row의 각 col의 의미는, 첫번째 토큰이 각 위치의 다른 토큰들에 대한 가중치 값이다. 동일한 가중치 값이, v의 각 col의 위치에 곱해짐. 그리고 이때 마스킹 된 부분이 사실상 v의 패딩에 내적 되면서 v의 패딩이 최종 결과에 아무런 영향을 미치지 않게 됨. 하지만 여전히 문제가 되는 부분은 왼쪽 softmax(mask(Q @ K.T)))행렬의 빨강 부분. 이전에 패딩과 내적된 row이다. 패딩 정보가 들어가 있음. 이 부분도 무시되어야 하는데…

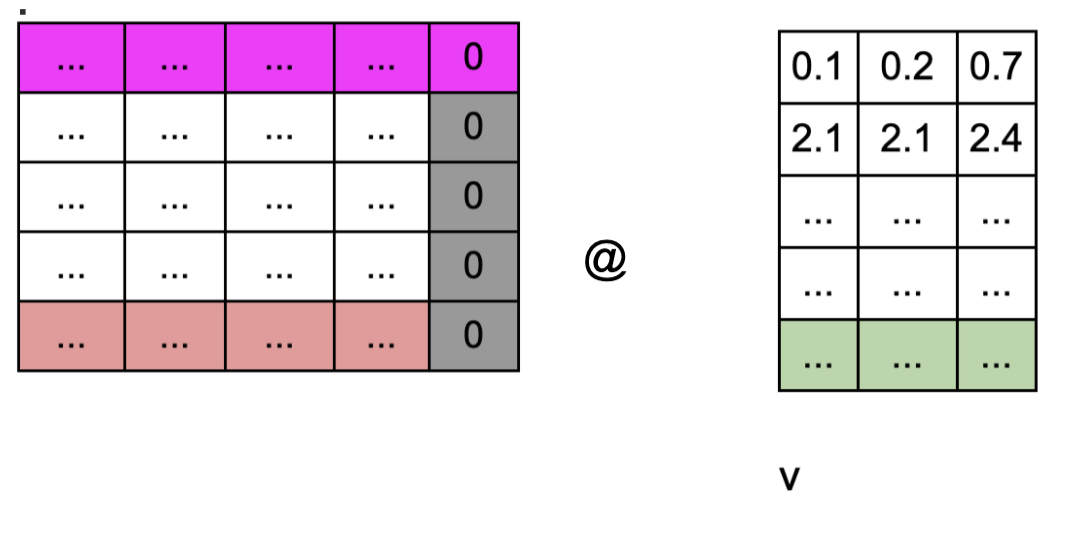
1. 각 row는 해당 위치의 토큰이 다른 토큰들과의 유사성에 대해서 가중평균된 값이다. 즉 해당 토큰이 특정한 의미 값으로 표현됨표현됨. attention된 hidden representation이 된다. 위의 빨강 패딩 정보가 들어간 부분을 보라색으로 표시함. 패딩이 다른 모든 토큰들과 가중 sum된 상태. masking으로 지우지 못함. 이 상태로 인코더 레이어를 여러번 통과하게 된다. 그런데 사실 맨 아래가 패딩인 이 상태는, 맨 처음 input의 패딩이 맨 아랫줄만 패딩 정보를 가지고 있는 것과 동일하다. 즉, 처음의 패딩 정보가 들어가 있는 row가 인코더를 다 통과하면서도 동일한 row에만 남아있다. 이렇게 되면 인코더의 pad mask을 디코더에 넘기면, 디코더에서 인코더의 패딩 위치를 파악해서 불필요한 패딩 정보를 마찬가지로 없앨 수 있을 것이다. 이제 디코더로 넘어가자.

1. 디코더: Q의 패딩이 두개라고 해보자

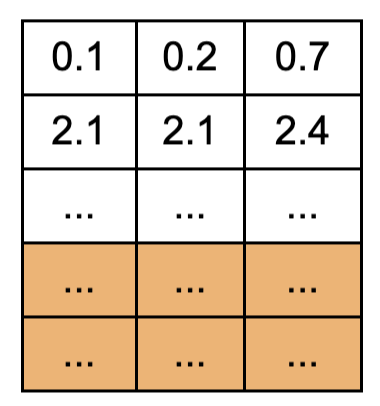
1. 인코더에서 넘어온 k, v

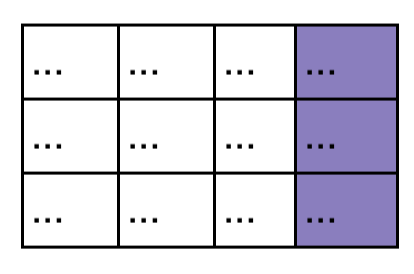
1. 디코더의 Q와 인코더에서 넘어온 K을 내적해서 유사도를 구한다. 그런데 인코더에서 넘어온 pad 부분이 여기서에서 인코더 pad mask와 합쳐져서 마스킹 됨. 디코더 패딩이 더 큰 부분은 디코더 패딩 마스크에서 걸러진다. 인코더 패딩 마스크랑 디코더 패딩 마스크랑 더 큰것으로 마스킹. 여기에서 인코더에서 미쳐 거르지 못한 부분이 마스킹된다. 따라서 주황색, 보라색 패딩 영역은 인코더에서 다뤘던 방식과 동일하게 진행되어서 레이어를 넘어가는 동안 패딩 정보가 다 없어짐. 결국 문제는 맨 아래 row에 있는 디코더 패딩이 다른 토큰들과 가중 sum된 부분만 남는다. 디코더 역시 마스킹을 Q, K에 대해서 두번하는게 아니라 한번만 하기 때문에 이런 문제가 발생함.

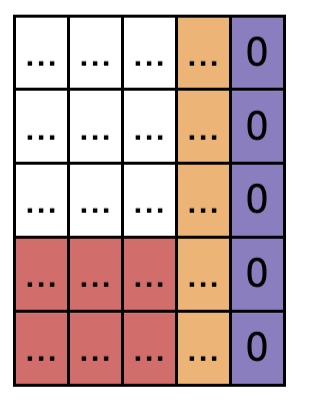
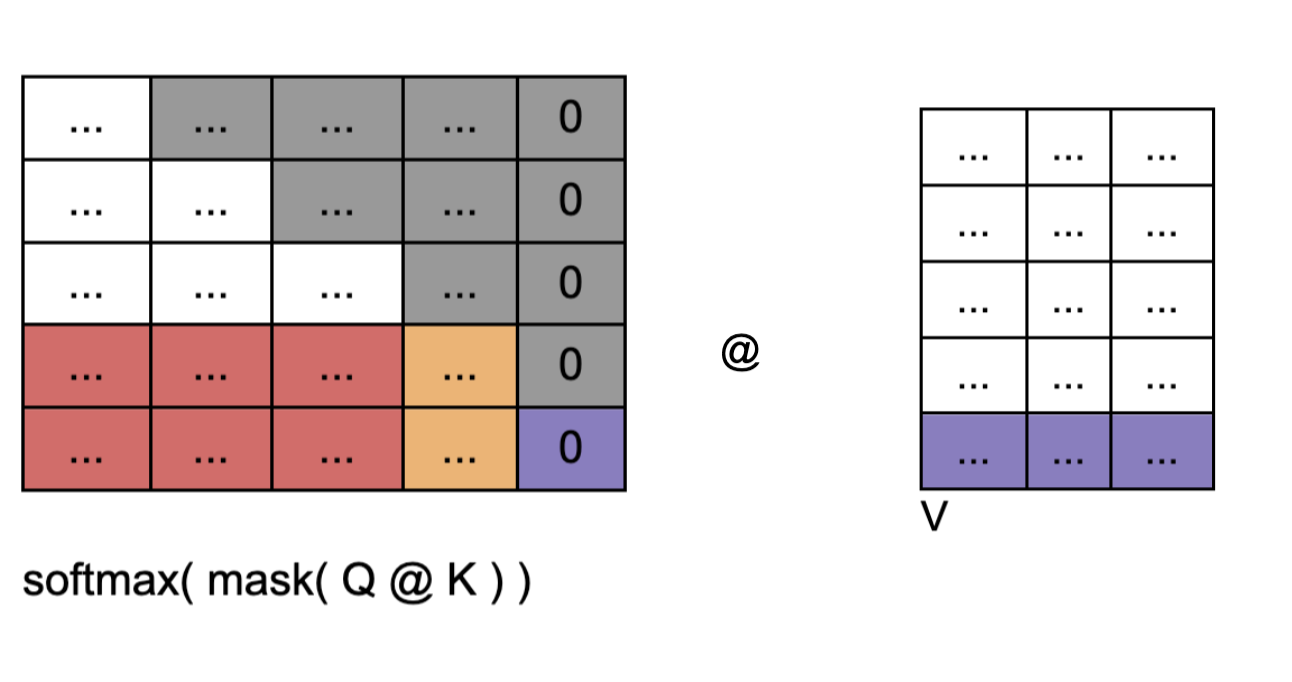
1. 그리고 여기에서 triangular mask도 겹쳐진다. 그리고 softmax( mask( Q @ K ) )

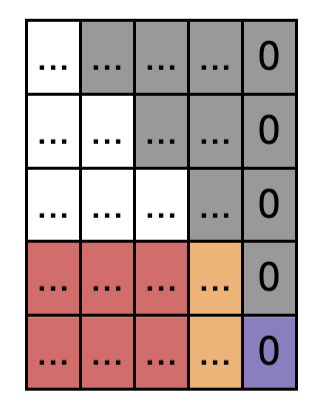
1. V는 인코더에서 넘어온 K와 동일한 행렬.

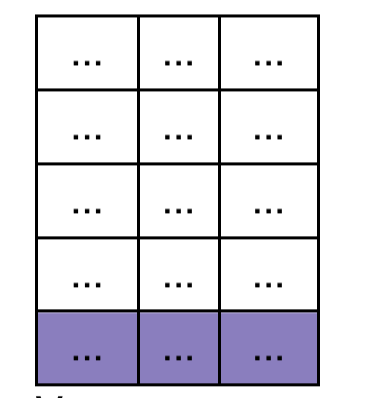
1. 모든 마스킹을 다 하고 softmax을 걸어서 가중치로 만든다. 그리고 V와 내적함. 인코더와 마찬가지로, 유사한 의미가 해당 토큰의 위치에 represent 된다.

1. (len, hidden_dim)이 다시 나오게 된다. 이 값이 최종적으로 디코더의 output으로 나오게 됨. 각 디코더 레이어를 나올 때 이 상황이 됨.

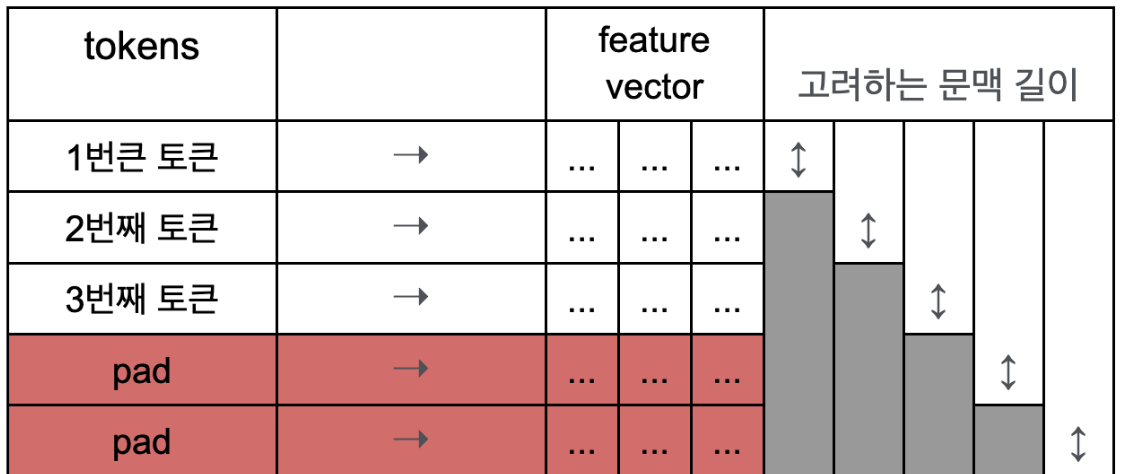
1. tri mask을 적용한 직관적인 의미: 2번째 토큰은 2번째까지만 문맥 반영해서 그 feature을 vector에 represent 한다. 3번째까지 문맥 반영해서 hidden represent. e.g. 1번째 토큰이 내적될 때, V에서 자기 자신에 해당하는 곳 말고는 마스킹 때문에 적용이 안됨.

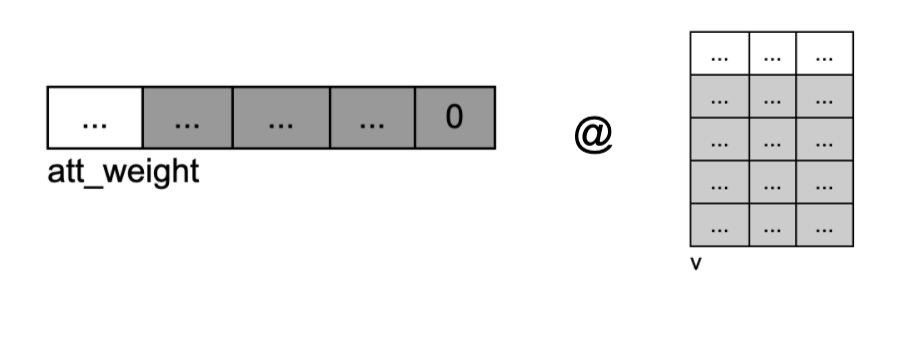
1. 최종적으로 디코더를 통과해서 나오는 행렬은 (len, hidden_dimension)이다. 마지막 linear layer을 타고 넘어가서 (len, num_token) 행렬이 나옴. 그리고 softmax을 걸어서 가장 높은 값으로 estimate 한다. 이때 반환 값은 index 값이다. 이 값이 모델의 최종 output이다. 그리고 이 값이 loss에 ground truth와 함께 넘어간다. 15번 최종 결과에서 나오는 패딩 row 이 과정 속에 그대로 포함되어 있다. 하지만 loss에 들어갈 때 argument으로 함께 넣는 CrossEntropy(output, target, ingnore_index = pad_idx)을 함께 넣으면, 실제 pad 위치인 빨강 row의 index는 학습에 사용하지 않고 그냥 무시함.
2. 이렇게 인코더의 패딩이 한 방향만 있을 때 발생하는 문제점은 디코더에서 소멸되고, 디코더에서 남아있는 패딩은 loss에서 무시하면서 해겨얼!

2. 디코더 self attention의 triangular mask의 직관적 의미

a. 배경

auto-regressive한 디코더를 만들기 위해서 masked self attention을 함. 뒤의 내용을 모르는 상태에서 예측하는 훈련임. 근데 실제 학습할 때는 이걸 동시에 triangular mask으로 수행함.

b. 의문

동시에 하는데 이렇게 굳이학습할 필요가 있나?

c. 생각해본내용

tri mask을 적용한 직관적인 의미: . e.g. 1번째 토큰이 내적될 때, V에서 자기 자신에 해당하는 곳 말고는 마스킹 때문에 적용이 안됨. 따라서 output 행렬의 1번째 row의 의미는 그대로 나옴. 2번째 row는 2번째까지만 문맥 반영해서 hidden represent가 됨. 3번째까지 문맥 반영해서 hidden representation이 된다. 그래서 output은 각 토큰까지만 문맥을 반영한 hidden representation이라고 말할 수 있음. 이 과정은 디코더의 self attention에만 적용 된다. 이 결과가 Q 행렬이 되고, K와 V는 인코더에서 나옴. 인코더의 K와 V는 전체 모든 맥락을 다 포함해서 hidden representaion되어 있음. 디코더의 각 토큰과 가장 의미가 유사한 V의 각 토큰에 hidden representation에 누적되어 혼합 됨. 이때 현재 토큰의 위치까지의 feature에서 가장 유사한 정보들만을 인코더에서 가지고 올 수 있게 됨. 그래서 디코더의 특징이 그대로 유지된다. 이대로 반복되면서 최종 output 까지 감.

3. multihead attention의 구현과 개념이 다름?

a. 배경

논문에서와 구현할 때 multi head attention의 의미가 조금 다른 것 같음.

논문에서는 h_model을 다른 멀티 헤드로 보낼 때

Q,K,V을 각 i번째 linear layer 넣어서 축축소고, i번째 head에 넣는다. h개의 linear layyer와 h개의 head가 있음.

\[MultiHead(Q, K, V ) = Concat(head_1, ..., head_h)W^O \\ \text{ where } head_i = Attention(QW_i^Q, KW_i^K, V W_i^V)\] \[\text{Where the projections are parameter matrices } W_i^Q \in R^{d_{model}×d_k} , W_i^K \in R ^{d_{model}×d_k} , W_i^V \in R^{d_{model}×d_v} and W_O \in R^{hd_v×d_{model}}\]

구현에서는 linear에 넣을 때 d_model로 들어가서 d_model으로 나옴. 그 다음에 d_model을 쪼개서 sub vectorspace으로 나눈 다음에 multihead attention에 각각 집어넣음.

# given Q, K, V # (B, max_len, d_model)
Q = fc(Q) # (B, max_len, d_model)
Q = Q.view(B, max_len, num_head, d_k).transpose(1,2) # (B, num_nead, max_len, d_k)
Q, K, V = multihead(Q,K,V)
Q = Q.transpose(1,2).view(B, max_len, d_model)

def multihead(Q, K, V):
		return softmax( Q.matmul(K.T).masked_fill(mask) ).matmul(V) / sqrt(Q)

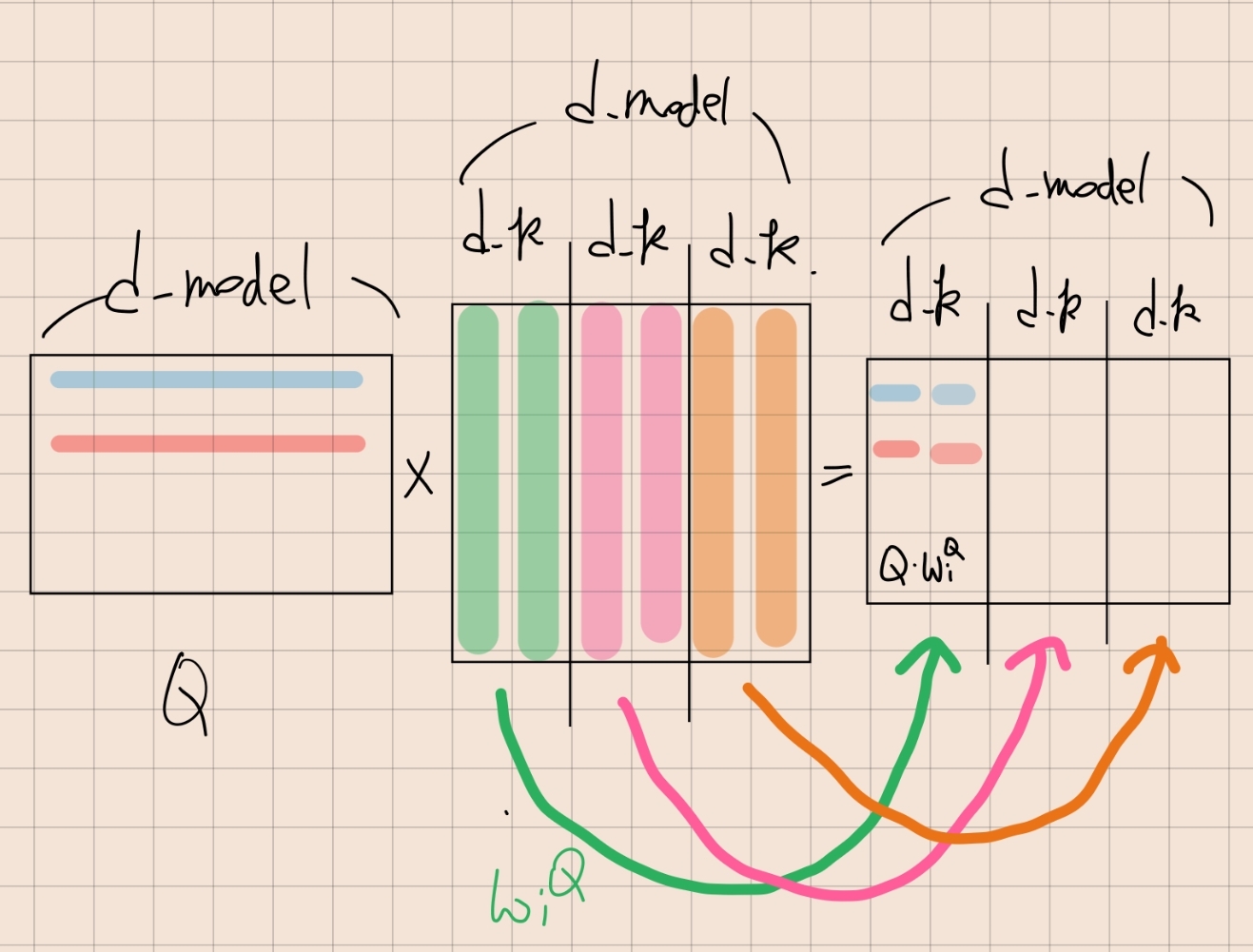
공부한 내용: 그런데 사실 이 두 내용은 동일하다. 논문에서는 동일한 Q을 h개의 linear으로 통과시키고 각 차원은 d_model에서 d_k으로 줄어든다. 구현에서는 동일한 Q을 linear layer으로 통과시키고 h개로 나눈다.

텐서의 모양을 살펴보면 알 수 있음. 가운제 weight matrix 의 차원이 d_model인데, d_k으로 column을 쪼개면, Q와 내적될 때 독립적으로 내적 됨. 각각의 d_k가 w_i가 된다.