DIFFERENTIAL TRANSFORMER review

DIFFERENTIAL TRANSFORMER

• https://arxiv.org/pdf/2410.05258

배경:

attention 메커니즘에서 attention 가중치가 불필요한 토큰에 걸리는 경우가 있음. 이 문제 때문에 성능 하락이 꽤 있다. 할루시네이션 등등등… 이것을 저자들은 attention noise라고 부른다.

가설:

전자공학 노이즈캔슬링과 같은 기술에서는 두 신호를 빼서 노이즈를 제거함. attention noise도 마찬가지로 두 attention을 구해서 빼면 노이즈를 없앨 수 있지 않을까?

we partition the query and key vectors into two groups and compute two separate softmax attention maps. Then the result of subtracting these two maps is regarded as attention scores. The differential attention mechanism eliminates attention noise, encouraging models to focus on critical information.

The approach is analogous to noise-canceling headphones and differential amplifiers [19] in electrical engineering, where the difference between two signals cancels out common-mode noise.

실험:

• decoder-only model
• 기본 attention 레이어과 아주 유사함. 어텐션 블럭 자체만 수정하고 나머지 동일하게 트랜스포머 아키텍처 유지함.
  • L개의 diff attention 레이어
  • 입력 토큰 \(x=x_1 \cdots x_N\)
  • 임베딩 레이어에 넣는다. \(X^0=\left[\boldsymbol{x}_1, \cdots, \boldsymbol{x}_N\right] \in \mathbb{R}^{N \times d_{\text {model }}}\)
  • 임의의 레이어의 입력 혹은 출력: \(X \in \mathbb{R}^{N \times d_{\text {model }}}\)
    • 일반적은 transformer: q,k,v가 들어오면 현재 레이어에서 동일한 embedding 유지하면서 linear layer 한번 태움.
    • diff attention: linear layer 태우는 것은 동일하지만 두개의 attention을 수행함. 따라서 linear projection을 할때 두배 크기로 늘림. 두배로 늘린 다음, 쪼개서 일반적인 transformer의 attention과 동일한 dimension 크기로 attention 수행함.
      • \(W^Q, W^K, W^V \in \mathbb{R}^{d_{\text {model }} \times 2 d}\): 각각 query, key, value vector에 projection 할 linear. 두개의 attention으로 쪼개야 해서 2d 으로 늘린다.
      • \(Q_1, Q_2, K_1, K_2 \in \mathbb{R}^{N \times d}, V \in \mathbb{R}^{N \times 2 d}\): Q1,K1는 첫번째 attention 연산, Q2, K2는 두번째 attention 연산. 각각 일반적인 transformer과 동일한 크기이기 때문에 dimension 크기 d이다. V의 경우 두개의 attentoin 연산에 각각 element-wise multiplication해야 하기 때문에 2d이다.

  \(\) \begin{gathered}{\left[Q_1 ; Q_2\right]=X W^Q, \quad\left[K_1 ; K_2\right]=X W^K, \quad V=X W^V} \ \operatorname{DiffAttn}(X)=\left(\operatorname{softmax}\left(\frac{Q_1 K_1^T}{\sqrt{d}}\right)-\lambda \operatorname{softmax}\left(\frac{Q_2 K_2^T}{\sqrt{d}}\right)\right) V\end{gathered} \(\)

  • 일반적인 transformer과 마찬가지로 각각의 attention 연산에 각각 softmax해서 가중치를 몰아주고 정규화함. 2배로 늘린 V을 …? elementwise하면 같은 크기 되어서… d만 있으면 되는 것 아닌가?
  • 각각의 attention을 빼서 동일한 노이즈 값을 삭제한다. 삭제할 때 학습 가능한 가중치 lambda을 넣어서 최적값을 찾는다.
  • \[\lambda=\exp \left(\lambda_{\mathbf{q}_1} \cdot \lambda_{\mathbf{k}_1}\right)-\exp \left(\lambda_{\mathbf{q}_2} \cdot \lambda_{\mathbf{k}_2}\right)+\lambda_{\text {init }}\]
  • \[\lambda_{\mathbf{q}_1}, \lambda_{\mathbf{k}_1}, \lambda_{\mathbf{q}_2}, \lambda_{\mathbf{k}_2} \in \mathbb{R}^d\]

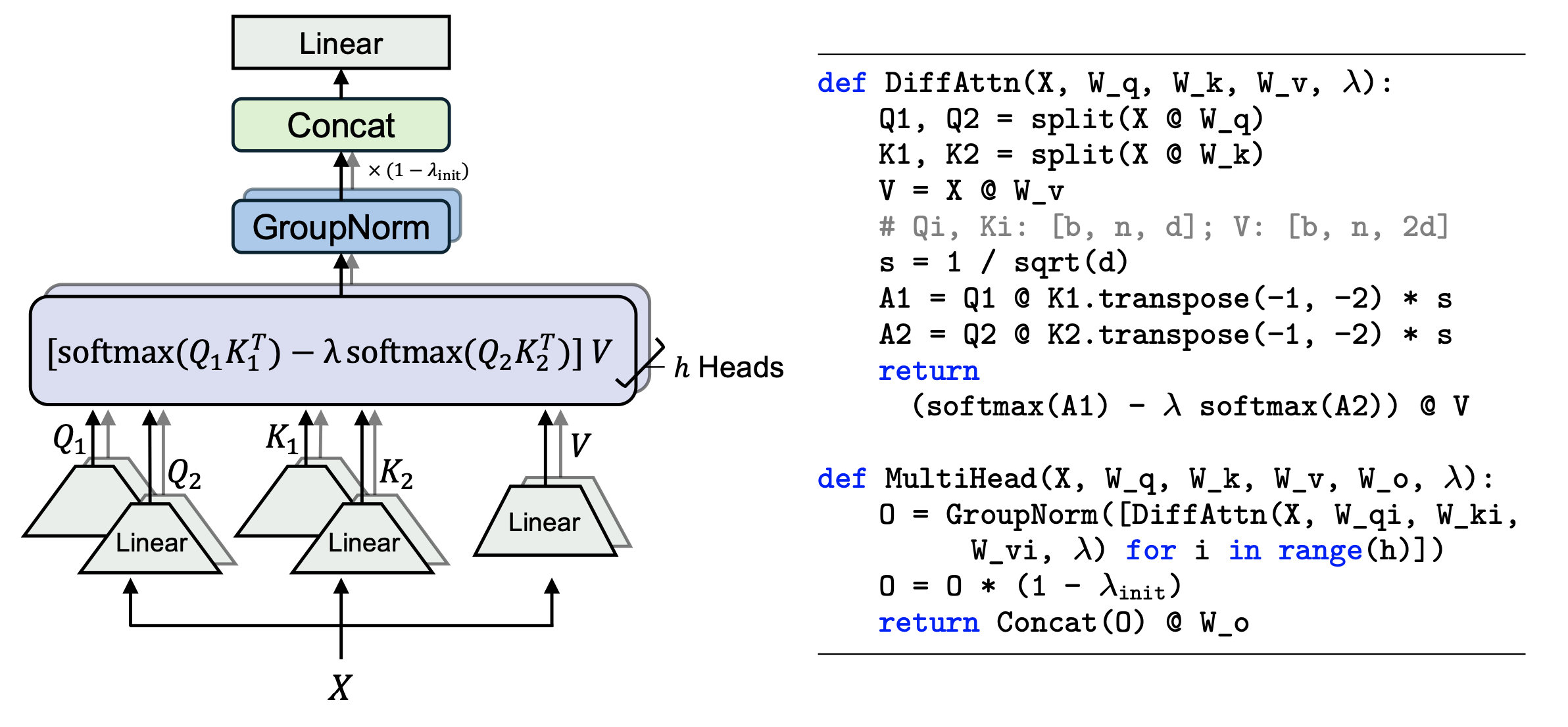
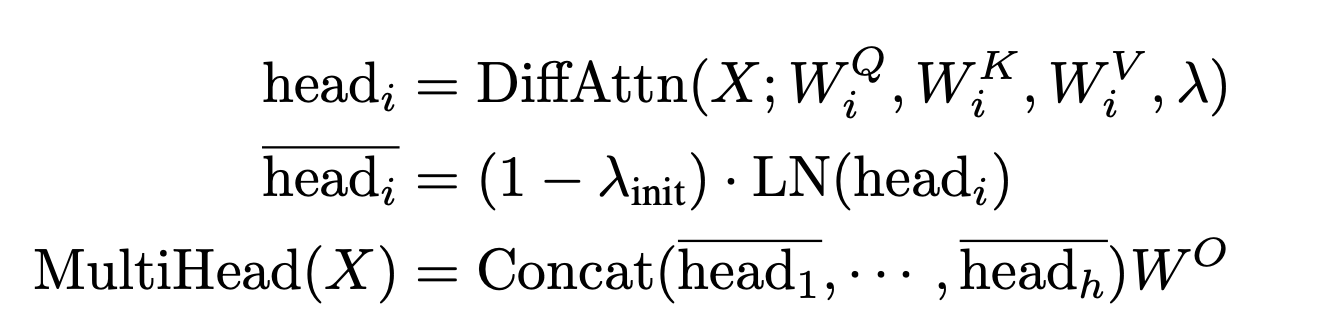
• llama을 따라서 nomalization 및 정규화함ㅎ수 설정ㅇ함.
  • adopt pre-RMSNorm [46] and SwiGLU [35, 29] as improvements following LLaMA

결론

• in context learning 에서 robustness 증가함.

• NLL loss 감소함

  

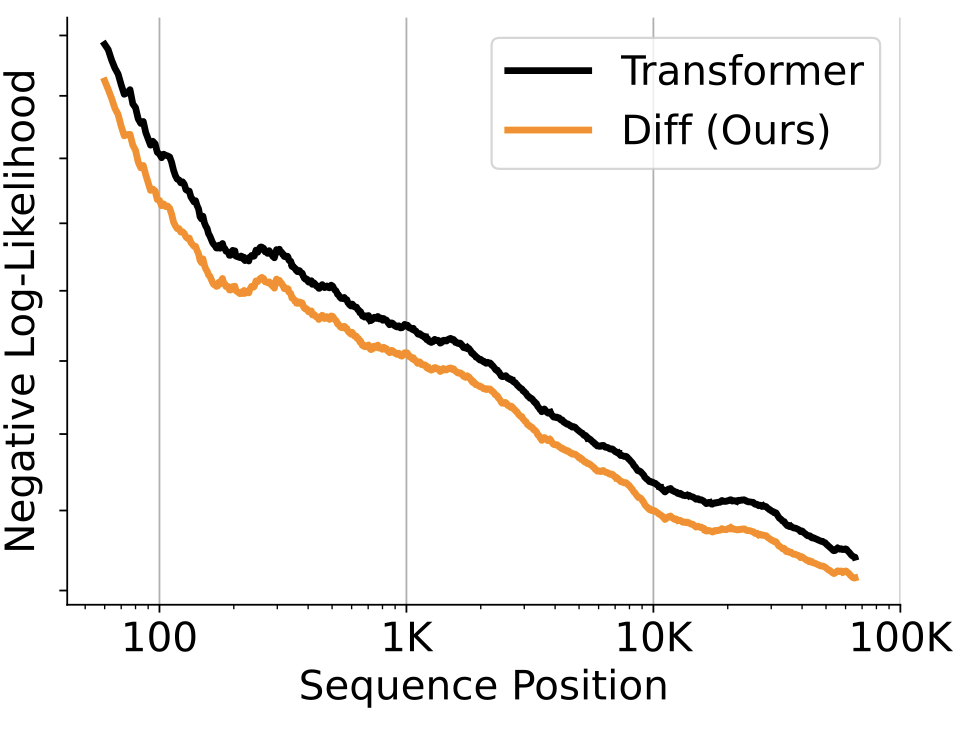
• training 더 효율적

  

  

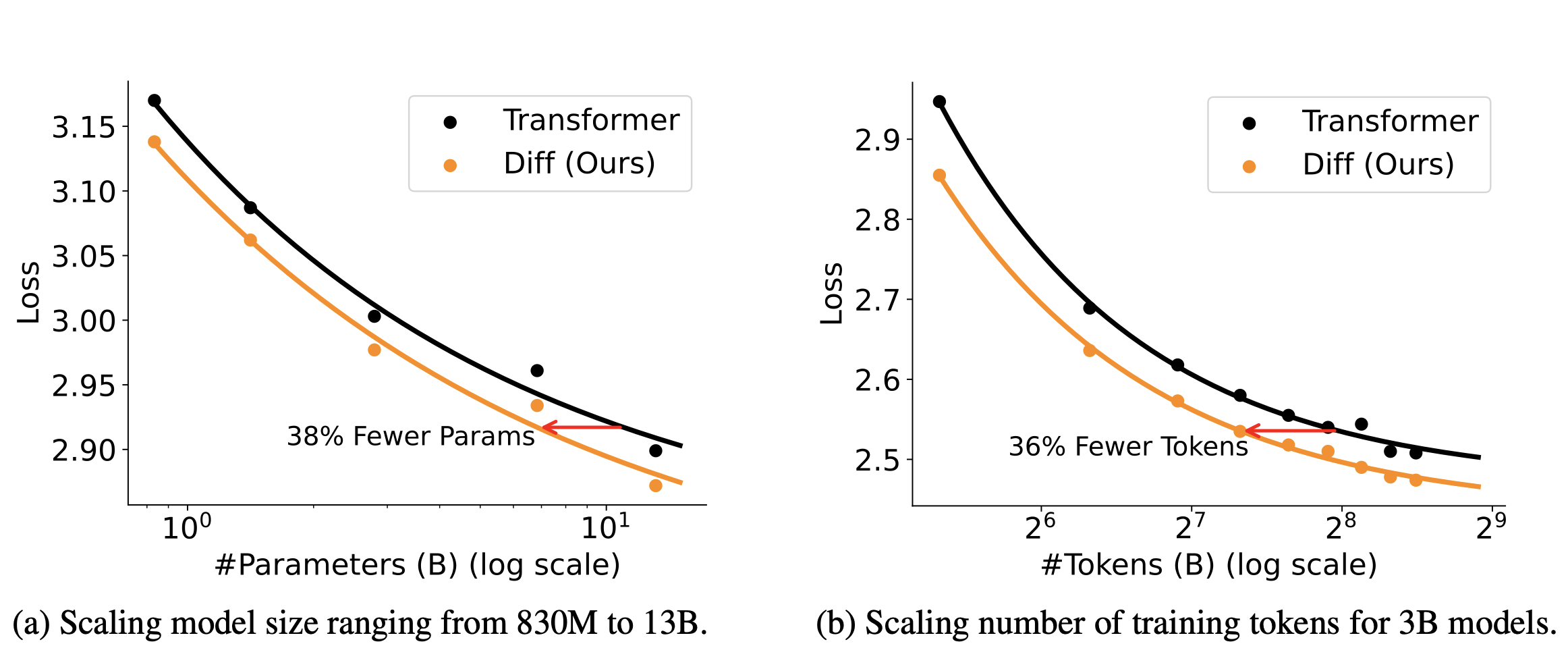
토의

• 질문: Weight 크기가 2d가 되었는데 그러면 필요한 메모리 양이 늘지 않나? 완전 2배는 아니더라도 꽤 커질 것 같은데… 성능이 높아지는대신 차지하는 메모리가 trade off cost으로 들어가는 것? 그 성능 대비 커지는 메모리 비율은 어느정도?

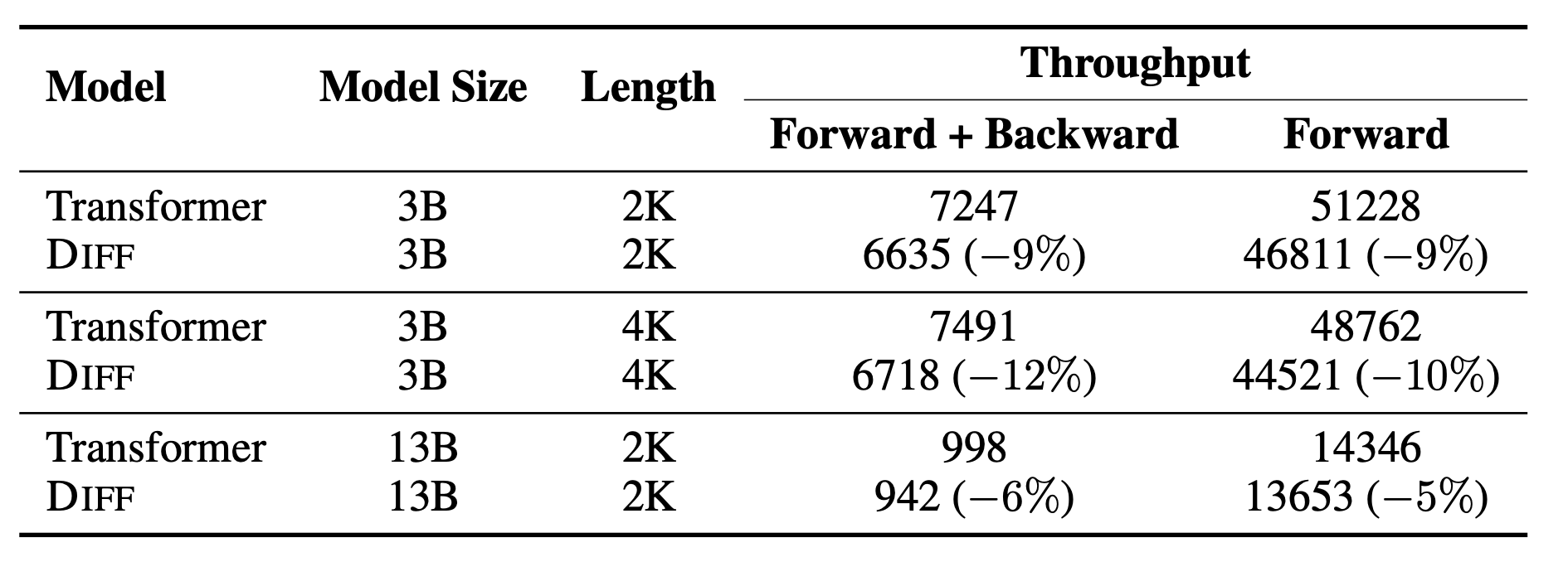
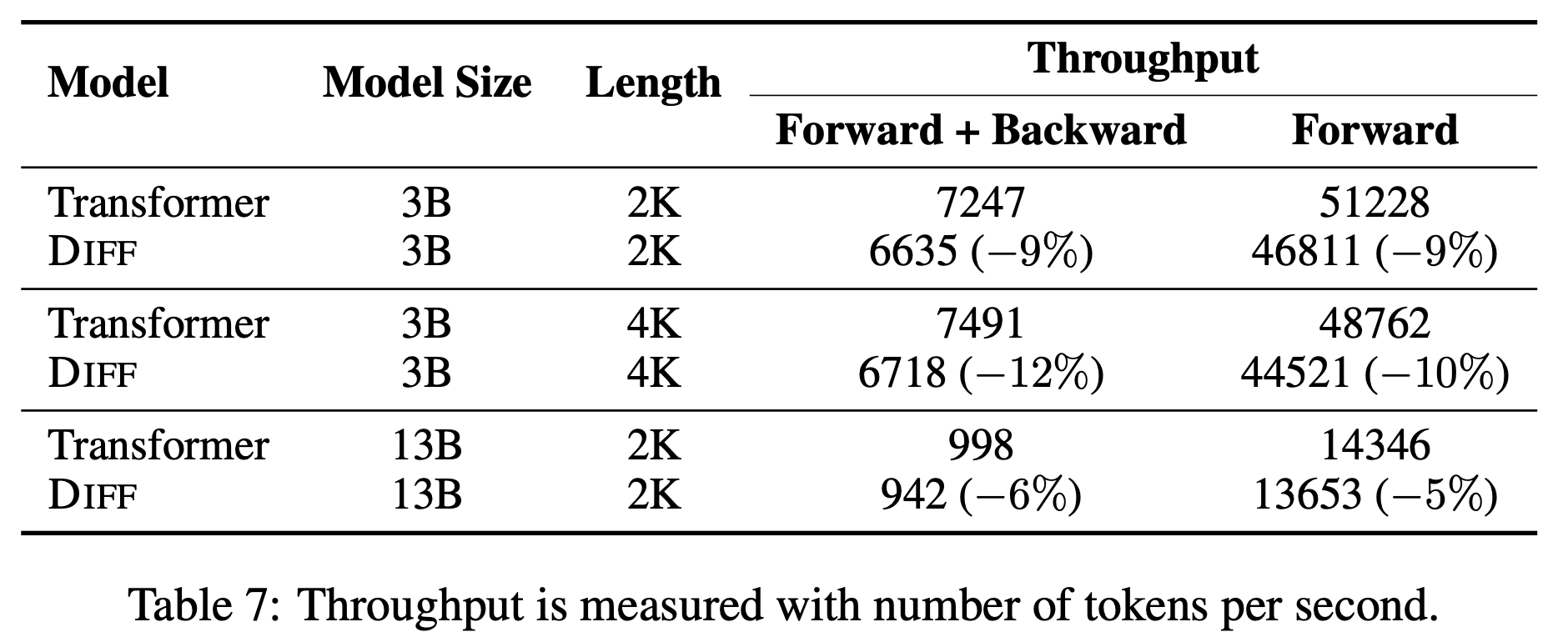
  throughtput 속도 비교 논의와 유사함. diff attention의 경우 atthen을 두개를 쓴다. 대신에 head의 수를 절반으로 줄임. 결과적으로 전체 메모리의 양이 동일함.

• table을 보면 cost efficiency을 보임. 4%~9%의 효율성 증가가 있음. 차지하는 메모리는 많아졌는데 어떻게 troughput이 더 많아질 수 있는가

  diff attention의 경우 atthen을 두개를 쓴다. 대신에 head의 수를 절반으로 줄임. 결과적으로 전체 메모리의 양이 동일함. 그러면서 동시에 throughput을 더 빠르게 향상시킬 수 있음. 더 적은 loss 결과를 보임. 더 높은 성능 및 robustness을 보임.

  

• 질문: 사실 굉장히 간단한 아이디어. 그냥 attention 연산 두개 만들어서 빼게 하기. 근데 그럼 두 attention 연산에서 두개 다 잘 잡으면? noise만 빼는 것이 어떻게 가능한가? 이게 왜 되지? 두 attention이 노이즈를 동일하게 가져야 하고, 실제 attention이 필요한 내용은 다르게 가져야 함. 이것을 어떻게 제어하는가? 어떻게 두 attention이 동일하게 동작하지 않을 것을 제어할 수 있으며 어떻게 동일하지 않게 동작하도록 제어할 수 있는가? 기존의 loss을 통한 gradient으로 제어가 가능한가?

  논문에서 어떻게 동작할 것이라는 가설 혹은 직관을 제시하지는 않음. 기존의 attention에서 noise가 발생해서 loss을 없앨 수 없는 것이 있었다면, 두 attention score의 차이라는 새로운 flow을 열어줌으로써 추가록 noise을 제거할 수 있게 해줌. 결과적으로 loss을 낮출 수 있다고 해석할 수 있어보임.

• 실험 결과만 본다면 무조건 하는게 좋아보이긴 하지만 언제나 그렇듯이 모든 도메인과 task에 대해서 적용가능할지는 직접 실험해보아야 알 수 있을 것. flash attention, multi-query attention처럼 앞으로 나올 모든 모델에도 적용될 수 있을까?

구현:

https://github.com/microsoft/unilm/blob/master/Diff-Transformer/multihead_diffattn.py

# class MultiheadDiffAttn(nn.Module): 
# method에 관계없이 이해하기 쉬운 순서로 재구성함

self.q_proj = nn.Linear(embed_dim, embed_dim, bias=False)
self.head_dim = embed_dim // num_heads // 2
# 2 * self.num_heads * self.head_dim == embed_dim
# attention 두개 * head로 쪼개서 attention * head 마다 dimension 수

self.n_rep = self.num_heads // self.num_kv_heads
# If it is not specified, will default to `num_attention_heads`.
# if self.num_kv_heads == self.num_heads, self.n_rep = 1. Reference: Lamma implementation. 
# https://github.com/huggingface/transformers/blob/main/src/transformers/models/llama/configuration_llama.py

self.k_proj = nn.Linear(embed_dim, embed_dim // self.n_rep, bias=False)
self.v_proj = nn.Linear(embed_dim, embed_dim // self.n_rep, bias=False)
# if self.num_kv_heads == self.num_heads, self.n_rep = 1. Same as self.q_proj

bsz, tgt_len, embed_dim = x.size()
q = self.q_proj(x)
q = q.view(bsz, tgt_len, 2 * self.num_heads, self.head_dim)
# 2 * self.num_heads * self.head_dim == embed_dim
q = q.transpose(1, 2)
# shape (bsz, 2 * self.num_heads, tgt_len, self.head_dim)

k = k.view(bsz, src_len, 2 * self.num_kv_heads, self.head_dim)
# if self.num_kv_heads == self.num_heads, same as q
# 각 토큰 마다 head 마다 representation vector

v = v.view(bsz, src_len, self.num_kv_heads, 2 * self.head_dim)
# if self.num_kv_heads == self.num_heads, heads에 2배 삭제됨. 대신 head_dim에 2배 붙음.
# 2 * self.num_heads * self.head_dim == embed_dim이라서 전체 노트 크기는 embed_dim으로 동일함. 

k = repeat_kv(k.transpose(1, 2), self.n_rep)
# if self.num_kv_heads == self.num_heads, self.n_rep = 1
# shape (bsz, 2 * self.num_heads, tgt_len, self.head_dim)
v = repeat_kv(v.transpose(1, 2), self.n_rep)
# if self.num_kv_heads == self.num_heads, self.n_rep = 1
# shape (bsz, self.num_kv_heads, src_len, 2 * self.head_dim)

attn_weights = torch.matmul(q, k.transpose(-1, -2))
# 크기 계산
# q shape (bsz, 2 * self.num_heads, tgt_len, self.head_dim)
# k shape (bsz, 2 * self.num_heads, self.head_dim, tgt_len)
# Att = q @ k.T attension shape ((bsz, 2 * self.num_heads, tgt_len, tgt_len))
# head 마다 각 토큰 마다 reprention이 있음. 다른 head의 representation과의 유사도 값(실수 범위)

# 몇몇 단계들 요약
# lambda 계산
# rotary embedding
# attention sqrt(head_dim) 계산 및 반영

# softmax at dim -1 -> 각 토큰 마다 head 마다 reprention이 있음. 다른 head의 representation과의 유사도 값 정렬화 [0, 1]
attn_weights = F.softmax(attn_weights, dim=-1, dtype=torch.float32).type_as(
  attn_weights
)

attn_weights = attn_weights.view(bsz, self.num_heads, 2, tgt_len, src_len)
# tgt_len == src_len

attn_weights = attn_weights[:, :, 0] - lambda_full * attn_weights[:, :, 1]
# 두개의 attention을 서로 뺀다. 첫번째 attention에서 두번째 attention을 뺀다! 
# 학습 가능한 가중치 lambda 만큼 적용함! 노이즈 제거!

attn = torch.matmul(attn_weights, v)
# attention shape (bsz, self.num_heads, tgt_len, src_len)
# value shape (bsz, self.num_heads, src_len, 2 * self.head_dim)
# matmul shape (bsz, self.num_heads, tgt_len, 2 * self.head_dim)

self.subln = RMSNorm(2 * self.head_dim, eps=1e-5, elementwise_affine=False)
attn = self.subln(attn)

attn = attn.transpose(1, 2).reshape(bsz, tgt_len, self.num_heads * 2 * self.head_dim)
# transpose shape (bsz, tgt_len, self.num_heads, 2 * self.head_dim)
# reshape shape (bsz, tgt_len, self.num_heads * 2 * self.head_dim)
# self.num_heads * 2 * self.head_dim == embed_dim
# shape (bsz, tgt_len, self.embed_dim)
# value의 dim을 두배로 늘린 것을 다시 합침

self.out_proj = nn.Linear(embed_dim, embed_dim, bias=False)
attn = self.out_proj(attn)