ResNet

Paper_Review_ResNet

https://arxiv.org/pdf/1512.03385.pdf

요약: 2015년에 나왔음. 레이어를 100이상으로 크게 늘려서 성능의 비약적 발전. vanighing gradient을 해결함. (Residual을 사용한 혹은 일반적으로도)기존의 연구에서는 layer가 깊어질 수록 vanishing gradient 때문에 trainig error 조차 증가하게 되는 문제점이 있다. 기존의 Residual과 Shortcut 연구를 활용. 에러가 감소하다가 다시 상승하는 기존의 문제를 해결. 해결방법: 최적 output의 결과를 identity mapping을 shortcut으로 사용하여 다음 layer에 집어넣는다. main path인 nonliniear path는 추가적인 정보를 학습한다. optimal input이 identity으로 전달되면 non linear layer의 weight은 0에 근사되어도 상관 없기 때문이다. layer의 깊이를 100 이상으로 두었을 때 non linear layer의 output이 0에 근사하는 것을 확인할 수 있었고, training error가 지속적으로 감소하는 것도 확인할 수 있다. 즉 optimal 정보가 identity mapping으로 전달된다는 것.

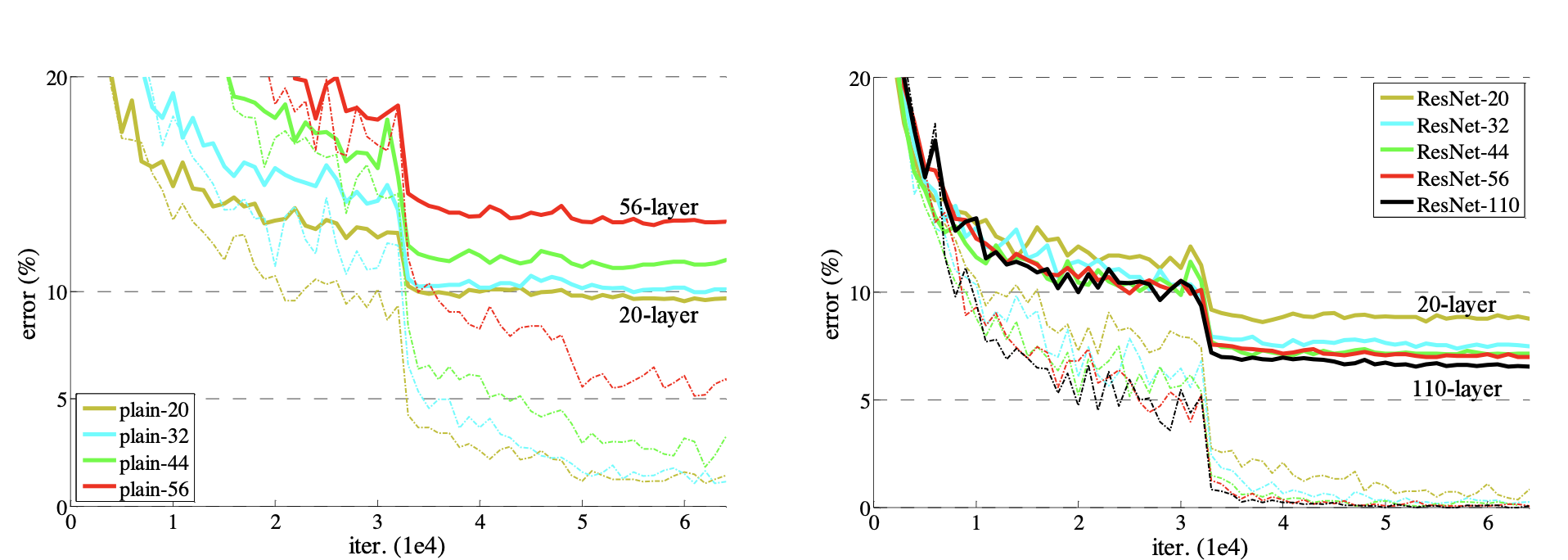왼쪽은 plain nn이고 오른쪽은 resnet이다. plain nn은 layer가 클 수록 에러가 커졌다. resnet은 layer가 클수록 에러가 감소함. bold는 test, 점선은 train error.

Iteratoin 2

Introduction

(Problem) When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher train- ing error, as reported in [11, 42] and thoroughly verified by our experiments. Fig. 1 shows a typical example.

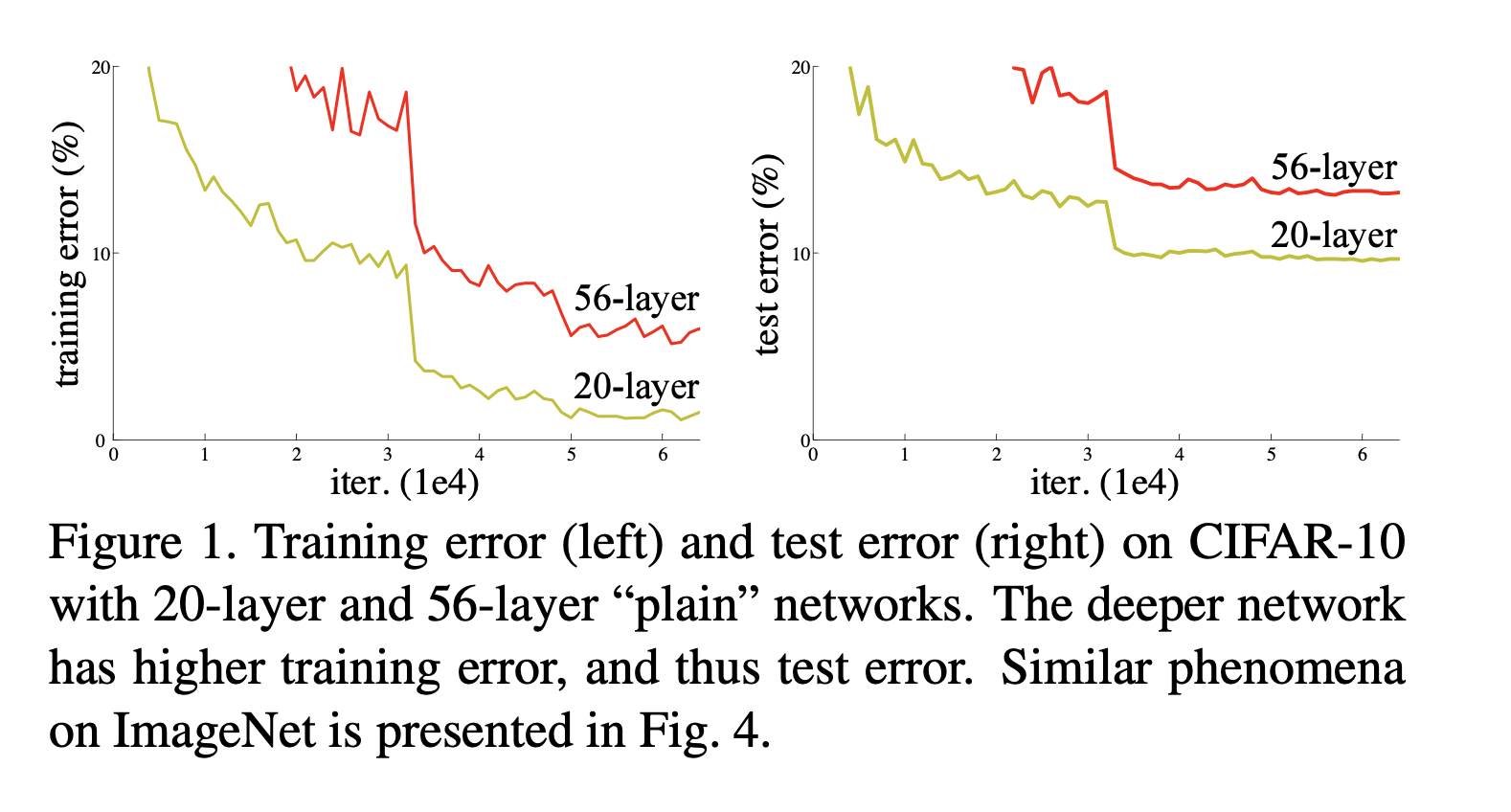왼쪽은 plain nn이고 오른쪽은 resnet이다. plain nn은 layer가 클 수록 에러가 커졌다. resnet은 layer가 클수록 에러가 감소함.

(Solution) There exists a solution by construction to the deeper model: the added layers are identity mapping, and the other layers are copied from the learned shallower model. The existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart.

But experiments show that our current solvers on hand are unable to find solutions that are comparably good or better than the constructed solution (or unable to do so in feasible time). 우리꺼 보다 더 좋은 solution을 찾지 못했다

In this paper, we address the degradation problem by introducing a deep residual learning framework.

we explicitly let these lay- ers fit a residual mapping.

Formally, denoting the desired underlying mapping as $H(x)$, we let the stacked nonlinear layers fit another mapping of $F (x) := H(x) − x$. The orig- inal mapping is recast into $F(x)+x$.

We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers. Original, optimal network H(x) 보다 같은 의미이지만 다른 표현인 F(x) - x을 최적화하느 것이 더 쉬울 것이라는 가정. 왜냐면 H(x)는 모양조차 모르는 가상의 가정된 최적 네트워크 구조이니까.

fig2

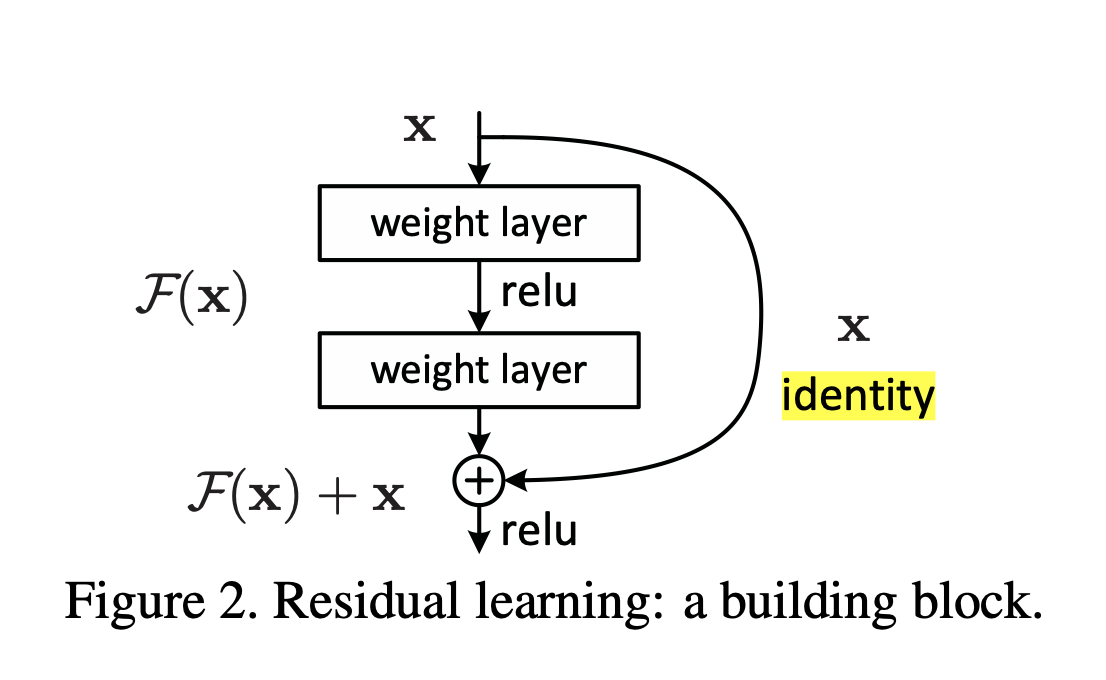
질문: 가상의 H에서 x을 뺀 것이 f이다. 그러면 f의 구조는 어떻게 아는가? 그리고 H에서 input x을 뺀다는 아이디어는 어디에서 왔는가? 왜 하필 x? residual에서 왔음.

fig2에서 기존의 네트워크를 f라고 한다. 그러면 f에 +x을 더하는 것이 최적이라는 가정은 어디에서 왔는가?

realized by feedfor- ward neural networks with “shortcut connections”

Shortcut connections [2, 34, 49] are those skipping one or more layers

In our case, the shortcut connections simply perform identity mapping

their outputs are added to the outputs of the stacked layers (Fig. 2).

given layere x, I(x) + (outputs of plain nn layers, maybe combination of functions.not to be single layer.)F(x)

The entire network can still be trained end-to-end by SGD with backpropagation, and can be eas- ily implemented using common libraries

figures: good performance. no training error rising up with deep layer. extremely deep layers from 100 to 1000.

Iteration 3

Related Work

Residual Representations Shortcut Connections

Shortcut Connections을 사용한 선행연구: gate을 사용했음. gate는 파라미터로 열리고 닫힘.

our identity shortcuts that are parameter-free our formulation always learns residual functions; all information is always passed through

이 논문은 residual을 gate 없이 항상 보내는 아이디어를 사용했음.

Deep Residual Learning

Residual Learning

Let us consider H(x) as an underlying mapping to be fit by a few stacked layers (not necessarily the entire net)

with x denoting the inputs to the first of these layers.

If one hypothesizes that multiple nonlinear layers can asymptoti- cally approximate complicated functions, then it is equiv- alent to hypothesize that they can asymptotically approxi- mate the residual functions, i.e., H(x) − x (assuming that the input and output are of the same dimensions).

만약 desired function H, 다른 말로 complicated function을 만들(근사할 ) 수 있다면(가정), residual이 있는 H(x) - x도 만들 수 있을 것이다. 좋은 함수 H에서 그냥 알고 있는 input x을 뺀 것이니까?

따라서 근사함수 H을 만들지 않고… residual이 있는 함수 H-x에 근사하겠다.

근데 어차피 H을 모르는데 어떻게 근사?

H -x = f. 우리는 f에 근사할 것이다. 따라서 원래 근사 함수 H = f+x가 된다.

근데 어쨌든 f가 뭔지 모르자나.

This reformulation is motivated by the counterintuitive phenomena about the degradation problem (Fig. 1, left).

fig 1 left: deeper layer has higher training error.

H가 shortcut with identity 으로 되려면… if the added layers can be constructed as identity mappings, a deeper model should have training error no greater than its shallower counter- part.

일단 H가 되어야 하니까… 깊어질 수록 error가 더 커지면 안된다.

기존의 연구에서 바로 이 문제가 불거졌던 것. 깊어질 수록 error가 커진다. 즉 H에 근사가 힘들어진다.

The degradation problem suggests that the solvers might have difficulties in approximating identity mappings by multiple nonlinear layers

기존의 연구에서는 (gate을 통한 )identity mapping이 H으로 근사하는 것이 f(x) 때문에 손상되었을 수도 있다.

With the residual learning re- formulation, if identity mappings are optimal, the solvers may simply drive the weights of the multiple nonlinear lay- ers toward zero to approach identity mappings.

만약 I(x)가 optimal 하다면, F(x)는 0이 되어도 충분. I(x)가 op이니까!

In real cases, it is unlikely that identity mappings are op- timal, but our reformulation may help to precondition the problem.

현실에서 I(x)가 optimal하지 않을 가능성이 크다.

If the optimal function is closer to an identity mapping than to a zero mapping, it should be easier for the solver to find the perturbations with reference to an identity mapping

그래도 I(x)가 optimal 정보를 가지고 있으면 non linear multiple layers f(x)을 구현하는 것보다 훨씬 쉬울 것. I(x)만 관리하고 f(x)는 0에 가까운 값을 주면 된다.

We show by experiments (Fig. 7) that the learned residual functions in general have small responses, suggesting that identity map- pings provide reasonable preconditioning.

fig 7에서 residual function이 작은 반응을 가진다? 그래서 I(x)가 납득할 만한 조건을 준다? 뭔소리?

3.2. Identity Mapping by Shortcuts

adopt residual learning to every few stacked layers.

\[y = F(x, {W_i}) + x \cdots (1)\]

The dimensions of x and F must be equal in Eqn.(1). If this is not the case, we can perform a linear projection Ws by the shortcut connections to match the dimensions:

\[y = F(x, {W_i}) + W_sx \cdots (2)\]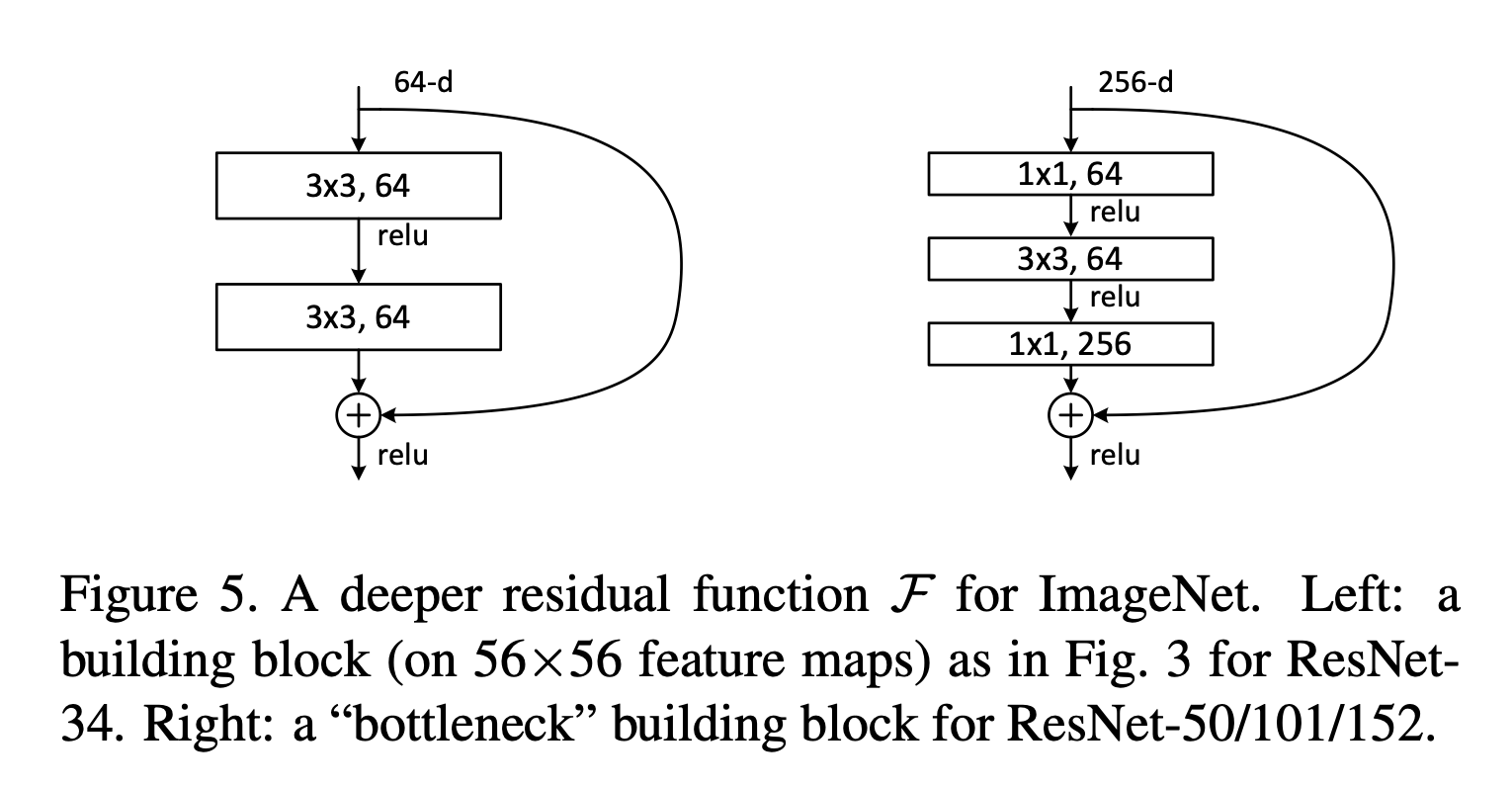

The form of the residual function F is flexible. Exper- iments in this paper involve a function F that has two or three layers (Fig. 5),

wo or three layers (Fig. 5), while more layers are possible. But if F has only a single layer, Eqn.(1) is similar to a linear layer: y = W1 x + x, for which we have not observed advantages.

3.3. Network Architectures

We have tested various plain/residual nets, and have ob- served consistent phenomena.

we consider two options: (A) The shortcut still performs identity mapping, with extra zero entries padded for increasing dimensions. This option introduces no extra parameter; (B) The projection shortcut in Eqn.(2) is used to match dimensions (done by 1×1 convolutions).

3.4. Implementation We use a weight decay of 0.0001 and a momentum of 0.9 and others…

fig 7

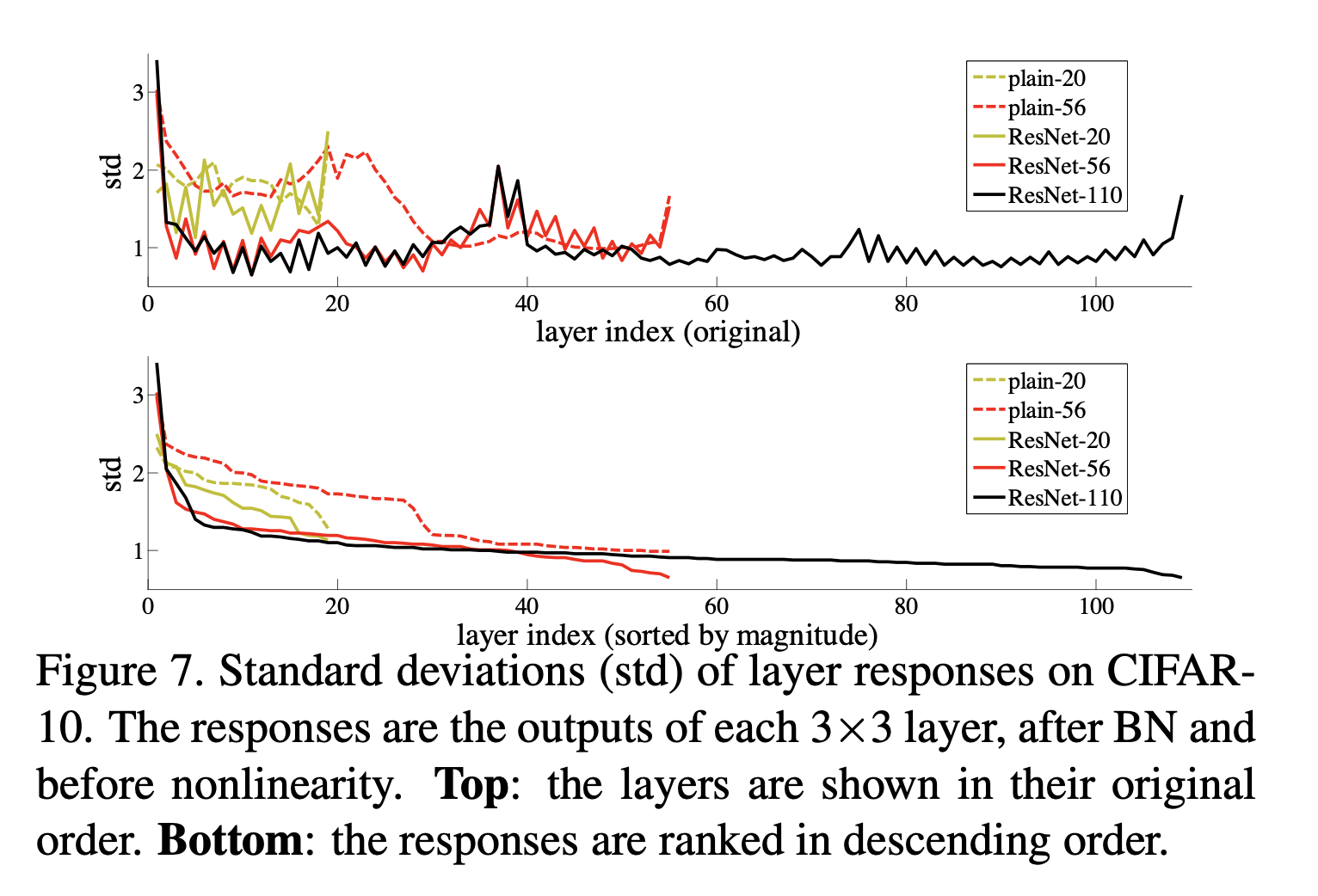
layer가 커질 수록 residual function f(x)의 output은 0에 수렴하는 것을 확인할 수 있음. motivation이 만족되는 것을 확인할 수 있었다.