Paper_Review_Batch-Normalization

Batch Normalization Sergey Ioffe at al. 리뷰

Reference

https://arxiv.org/pdf/1502.03167.pdf

Problem Statement

• (external) Covariate Shift
  • input X으로 신경망을 학습
  • 그런데 만약 X의 distribution이 바뀌면 학습이 어려워진다.
  • sigmoid activation을 예로 들어보자.
    • 한번은 z가 -7이었는데, 다음 번에는 +9이다.
    • z의 값에 따라 a의 값도 변동이 심하다.
    • dW = dZ dot A
    • $W = W - \alpha \cdot dW$
    • W의 변동이 커져서 학습이 어려워 진다. 증가 했다가 감소했다가… 학습이 느려질 것.
• In- ternal Covariate Shift.
  • Z = W dot A + b
  • 그런데 여기서 A는 또 다시 이전의 Z의 영향을 받는다.
  • 이렇게 모든 뉴런들은 이전의 값들에 영향을 받는다.
  • 이전 레이어에서 값의 변동이 커져서 한번 출렁이면 계속 출렁거리게 된다.
• 결국 external 이든 internal 이든 값의 변화가 커지면 학습이 느려진다.
• 혹시 변동을 줄일 수 있을까?

Idea : Normalize을 하자!

• m개의 date example이 있을 때
• $z \in R^{n_l \times m}$
• 1개의 레이어, 1개의 노드에 대해서 먼저 생각해봄.
• 하나의 노드에 1개의 z가 들어온다.
• m개의 example이 독립적으로 계산된다. 마지막 output node에 가서 더해진다.
• 출렁거린다는 것은… 각 example 마다 아주 다른 z값을 들고 올 때 a의 값도 변화가 크고, dW = dZ dot A을 따라 w의 변동도 커지게 된다.
• m개의 z들을 평균하고 분산을 구한다. 그리고 정규화한다. $z_{norm}$
• 그러면 m개의 example이 0을 중심으로 std 1으로 고만 고만하게 들어올 것이다.
• $n_l$개의 모든 노드에서 같은 일이 발생한다.
• 모든 레이어에서 같은 일이 발생

문제점 : 모든 z가 0을 중심으로 분포

• 변동성은 줄였다.
• 그런데 사실 정규화를 하게 되면 활성화함수의 linear한 부분만을 사용하는 것이다. 아주 가끔 끝으로 가게 될 것…
• 활성화 함수를 사용하는 이유가 non linearity에 있는데 identity와 다를 것이 사라짐.
• 0을 중심으로 분포하는 것이 아니라 다른 값을 중심으로 분포하게 하고(shift) 분산의 크기도 변화시킬 수 있게 하자(scale).
• $z_{norm}$은 z의 (Gaussian Dist에서 쓰는)정규화이다. $k$번째 노드를 기준으로 $m$개의 eg들의 노드 output $z_k$의 분포를 정규화
• 이를 위해 새로운 파라미터를 적용. $\gamma, \beta$
• $\beta$는 각 노드에서… $z_{norm}$의 평균 값의 의미이다. $\gamma$는 기준 분산 값이다. k번째 노드에서 $\tilde z_k = \gamma_k \cdot z_{norm,k} + \beta_k$. m개의 example이 같은 $\gamma$와 $\beta$을 사용하는 것이다. $\gamma$와 $\beta$는 모델이 학습하는 파라미터이다.
• Batch Normalization으로 transformation하는 것으로도 생각할 수 있다.
• $z_{norm}$이 0을 기준으로 정규화되었으므로, $\gamma$와 $\beta$의 결과로 나온 $\tilde z$도 특정한 구간에서만 발생한다. $\beta$을 기준으로 $\gamma_k \cdot z_{norm,k}$의 구간에서만 발생.

\[\begin{aligned} z & = W a, z \in R^{n_l}\\ z_{norm} & = norm(z), z_{norm} \in R^{n_l}\\ \tilde z & = \gamma \cdot z_{norm} + \beta\\ a & = g(\tilde z)\\ \end{aligned}\]

• 이것을… a와 z 사이에 sub network가 하나가 더 있다고 생각할 수 있다. 각 레이어에서 각 노드에 각각의 독립된 네트워크가 하나 씩 있는 것. 그리고 학습할 때 그 파라미터인 $\gamma$와 $\beta$도 학습하는 것이다. 학습을 통해서 비용함수를 극소화하는 Activation function에서 가장 적절한 평균과 분산을 찾아낸다.

# Plain NN
W - z - a - ... - L
a //    W //
b /     b /

# Batch Normalization NN
W - z - z_norm - z_telde - a - ... - L 
a /      gamma //          w /
         beta  /

• 조금 더 명화하게 써보면… m개의 training example이 있을 때

\[\] \[\begin{aligned} Z & = (z^{(1)} \cdots z^{(i)} \cdots z^{(m)}), z^{(i)} \in R^l\\ \mu & = \frac{\sum_i^m z^{(i)}}{m}\\ \sigma^2 & = \frac{(\sum_i^m (z^{(i)} - \mu))^2}{m}\\ z_{norm} & = \frac{z^{(i) - \mu}}{\sqrt{\sigma^2 + \epsilon}}, \epsilon \ge 0\\ & \text{for single example, }\\ z & = W a, z \in R^{n_l}\\ \tilde z & = \gamma \cdot z_{norm} + \beta, \text{ s.t. } \gamma, \beta \in R^{n_l}\\ a & = g(\tilde z)\\ J & = \sum_i^m \mathcal{L}(\hat y_i, y_i)\\ \frac{\partial L}{\partial W} & = \frac{\partial L}{\partial z} \frac{\partial z}{\partial w}\\ \frac{\partial L}{\partial z} & = \frac{\partial L}{\partial \tilde z} \frac{\partial \tilde z}{\partial z_{norm}}\frac{\partial z_{norm}}{\partial z}\\ \frac{\partial L}{\partial \gamma} & = \frac{\partial L}{\partial \tilde{z}} \frac{\partial \tilde{ z}}{\partial \gamma}\\ \frac{\partial L}{\partial \beta} & = \frac{\partial L}{\partial \tilde{z}} \end{aligned}\\\]

• 계산 결과(논문에 그대로 있어요!)

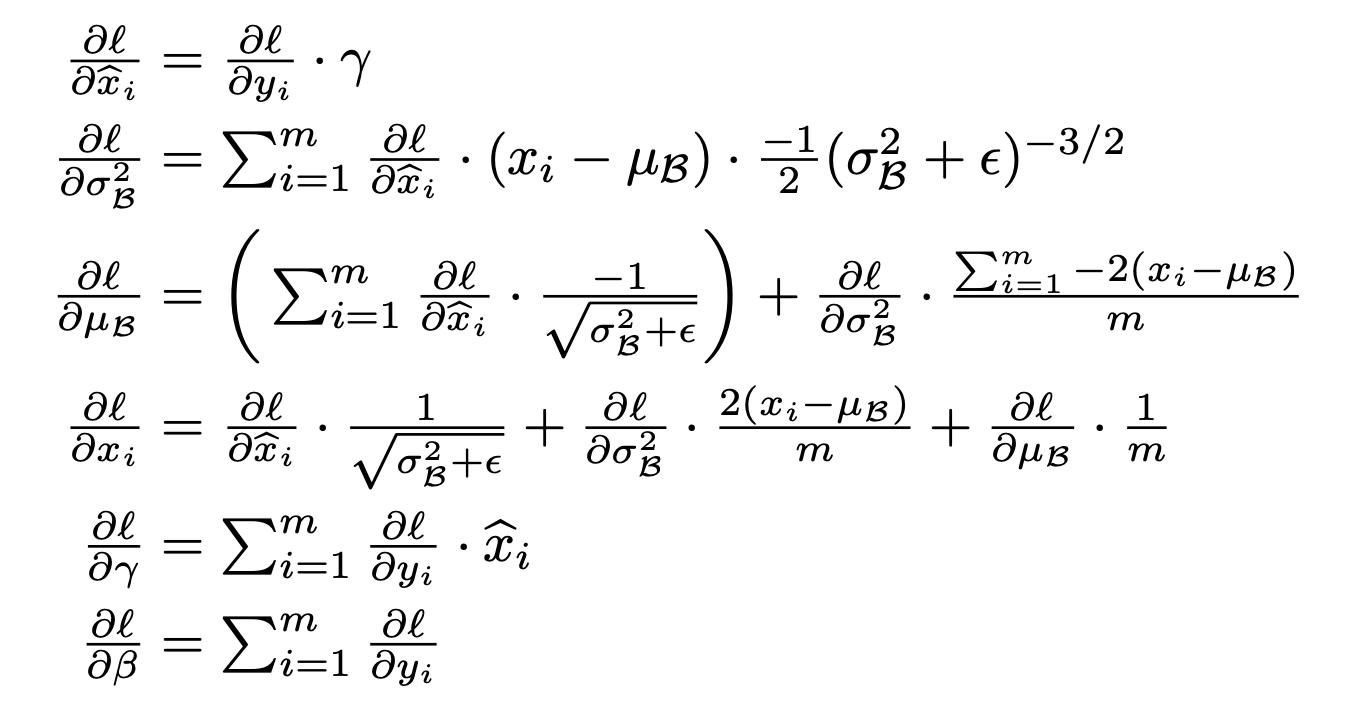
mini-batch

파라미터 학습

• 전체 training set뿐만 아니라 mini-batch에도 적용.
  • stochastic optimizer에 사용한다면 mini batch가 효율적.
• 전체 training set을 mini batch으로 나누고, 각 mini batch의 size을 m이라고 하자.
  • 파라미터를 1번 업데이트 할 때 m개의 exampe을 학습.
  • m개의 example들로부터 $z_{norm}$을 계산하고… 주어진 $\gamma$와 $\beta$을 사용해서 정규화, shift, scale한다.

• 알고리즘(논문에 그대로 있어요!)

• back propagation하면서 gamma와 beta도 update.
• 일반적인 mini batch GD을 할 때 W을 다음 배치에 그대로 사용하는 것처럼 gamma와 beta도 마찬가지. T개의 mini batch을 돌면서 모든 trainig set을 정규화하고 적절히 shift, scale할 gamma와 beta을 찾아낸다.

prediction

• $\gamma$와 $\beta$의 최적값을 찾아냈다.
• test을 할 때 z_norm은?
• train 할 때 각 mini batch 마다 z_norm을 구할 때 평균과 분산을 구했을 것이다.
• mini batch의 평균과 분산들의 평균을 구한다.
• Central Limit Theorem의 응용으로써 샘플의 평균의 평균은 모집단의 평균에 근사!
• 최근에는 일반적인 모평균과 모분산 추정이 아니라 exponential average을 사용하는 경우도 있는 것 같다(Andrew Ng 왈?)

• test set의 x을 feed forward 할때도 Batch Noramalization으로 transformation해야 한다.

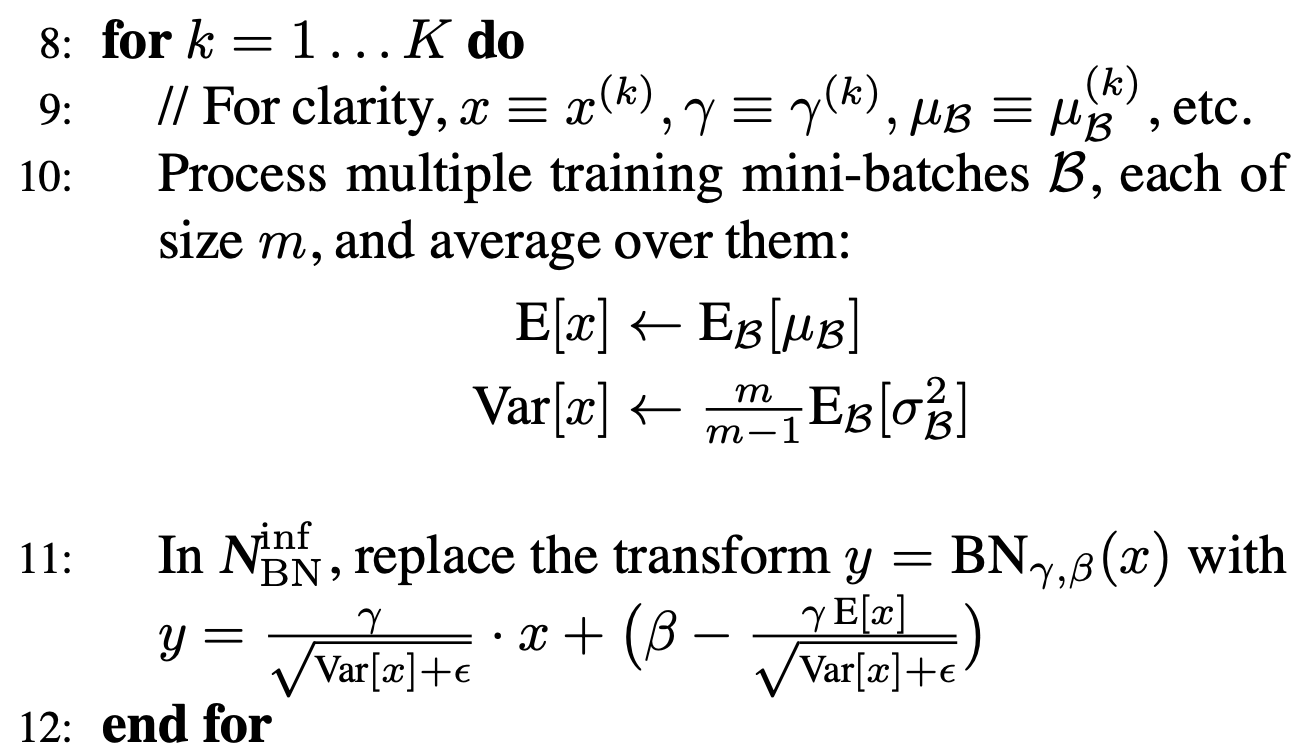
• batch nomalization transformation $y$. 이 $y$가 다음 레이어로 전달되는 것.
• 학습할 때 $y = \gamma \cdot z_{norm} + \beta$으로 다음 레이어로 전달했다. 예측할 때도 마찬가지로 transformation 해줘야 한다.
• 위에서 구한 $E[x], Var[x]$와 학습 결과로 얻은 $\gamma, \beta$을 사용한다. train network에서 사용한 $ㅛ = \gamma x + \beta$에 대입하면 11번이 나온다. 아래는 그 과정.

\[y = \gamma \cdot z_{norm} + \beta\\ z_{norm} = \frac{x - E[x]}{\sqrt{var[x]}}\\ y = \gamma \Big (\cdot \frac{x - E[x]}{\sqrt{var[x]}} \Big )+ \beta \cdots 11.\\\]

• epsilon > 0으로 divide by zero 방지.