BaekTree

Go Grow, Serve others.

7 minute read

optim

optim 이론 및 torch & huggingface 사용법

SGD

이론

Goodfellow의 DL 교과서에 따르면 sgd에서 자주 사용하는 adaptive lr은 linear learning rate이다. 아래 식을 따라서 lr이 decay 된다.

\[\epsilon_{k}=(1-\alpha) \epsilon_{0}+\alpha \epsilon_{\tau}\]

여기서 $\alpha = \frac{k}{\tau}$이다.

$e_0$: initial learning rate

$e_k$: k번째 iteration에서의 learning rate.

$e_{\tau}$: $\tau$ 번째 iteration을 지나고 나서 계속 유지하게 되는 lr. 보통 기존 lr의 1% 값이다. 따라서 보통 SGD을 쓰면 iter을 100번 동안 lr을 감소시킴. $\tau$ 번째 iteration을 지나면 $k = \tau$ 가 되어서 $\alpha = 1$이 됨. 그래서 앞 항이 사라지고 뒤항의 $\epsilon_{\tau}$만 남는다.

일반적으로 e_t가 e_0의 1%에 해당하는 값이고, 따라서 total_iters = 100 으로 둔다. 그러면 여기서 중점적으로 정해야 하는 것은 초기 lr인 e_0이다. Goodfellow는 휴리스틱하게 실험해보면서, 빠르게 떨어지면 값을 조금 줄이고, 잘 안떨어지면 값을 늘려보라고 권함.

용법

pytorch의 SGD 함수는 사실 진짜 SGD가 아니다. 그냥 loss에 던져지는 모든 데이터셋을 다 업데이트하고 option으로 momentum과 decay가 있을 뿐이다. 그래서 일반적인 mini batch 데이터로더에 사용하면 그냥 mini batch gradient descent이다. momentum만 사용할 수 있을 뿐. 그래서 실제 SGD을 쓰려면, 데이터로더에서 배치 크기를 1으로 하고, SGD을 사용해야 한다.

dataloader = DataLoader(dataset, batch_size= 1, shuffle=True)
optim = SGD(params, lr = e_0, ...)
for i = 0 to 100
	inputs, classes = next(iter(dataloader))
	outputs = model(inputs)
  loss(outputs, classes).backward()
	optim.step()

이론에서 적은 대로 SGD는 보통 linear lr decay을 사용한다.

사실 우리가 만들고 싶은 것은 iteration에 따라서 떨어지는 lr을 만들고 싶은 것. 이것은 사실 torch의 가장 기본 scheduler인 lambdaLR을 사용하면 구현할 수 있다.


# a = k / tau
# e_k = (1 - a) * e_0  + a * e_tau

# e_0 : initial lr
# tau: epoch number of decreasing lr
# e_k: lr in iteration k
# e_tau: constant lr after iteration tau

def lambda_func(epoch):
		
		e_0 = CONFIG['initial_lr'],
		e_tau = CONFIG['final_lr'],
	  tau = CONFIG['adaptive_epoch'],
		a = epoch / tau
		return (1 - a) * e_0  + a * e_tau

dataloader = DataLoader(dataset, batch_size= 1, shuffle=True)
optim = SGD(params, lr = e_0, ...)
scheduler = LambdaLR(optim, 
										lr_lambda=lambda_func(lambda_func)
						)

epoch = 100
for i in range(epoch):
	inputs, classes = next(iter(dataloader))
	outputs = model(inputs)
  loss(outputs, classes).backward()
	optim.step()
	scheduler.step()

그리고 linear lr decay는 pytorch에서 lr scheduler에 linear lr scheduler에서 지원함.

인줄 알았는데 torch의 linearLR은 initial LR으로 상승해가는 scheduler이다. 따라서 여기에 사용하면 안됨. 우리는 initaial LR에서 떨어지는 lr을 만들고 싶다.

https://pytorch.org/docs/stable/generated/torch.optim.lr_scheduler.LinearLR.html#torch.optim.lr_scheduler.LinearLR

*~~optimizer = SGD(parmas, lr = e_0, ...)*
schedular = torch.optim.lr_scheduler.LinearLR(
	*optimizer*, 
	*start_factor=0.3333333333333333*, # 0에서 1을 갈때 lr에 곱할 factor
	*end_factor=1.0*, # tau - 1에서 tau으로 갈때 lr에 곱할 factor
	*total_iters=5*, # 예제에서 tau. 실제 몇번의 iter 동안 업데이트 할것인지.  tau 후에 a = 1이 된다.
	*last_epoch=- 1*, 
	*verbose=False # 업데이트 할때마다 콘솔 출력*
)~~

예제의 SGD에 적용하면,

*~~optimizer = SGD(parmas, lr = e_0, ...)*
schedular = torch.optim.lr_scheduler.LinearLR(
	*optimizer*, 
	*start_factor = 1*, # 시작할 때 특별한 변화 없음. 그냥 쭉 linear
	*end_factor = 1*, # 끝날 때 특별한 변화 없음. 그냥 쭉 linear
	*total_iters = tau*, # 예제에서 tau. 실제 몇번의 iter 동안 업데이트 할것인지.  tau 후에 a = 1이 된다.
	*last_epoch=- 1*, 
	*verbose=False # 업데이트 할때마다 콘솔 출력*
)~~

SGD with momentum

이론

모멘텀은 특히 pooled condition hessian의 경우에 효과가 좋다. 즉 loss 함수의 contour가 타원일 경우에, gradient을 구했을 때 특정 방향이 다른 방향보다 더 많이 떨어져야 global minima으로 수렴하는 경우에 효과가 좋다. 모멘텀은 물리학의 뉴턴 법칙 analogy에서 나왔다. loss가 떨어지는 각 방향에서 loss가 떨어질 때 이전 epoch의 gradient 방향과 다음 방향이 같으면 적용할 gradient 값이 커진다. 즉, 관성을 가지도록 만들었다. 타원형 contour을 가질 때 관성이 있으면, oscilliation이 많은 방향은 점차 줄어들고, 실제로 global minima에 도달해야 하는 방향으로는 관성이 생겨서 더 빠르게 이동하게 된다.

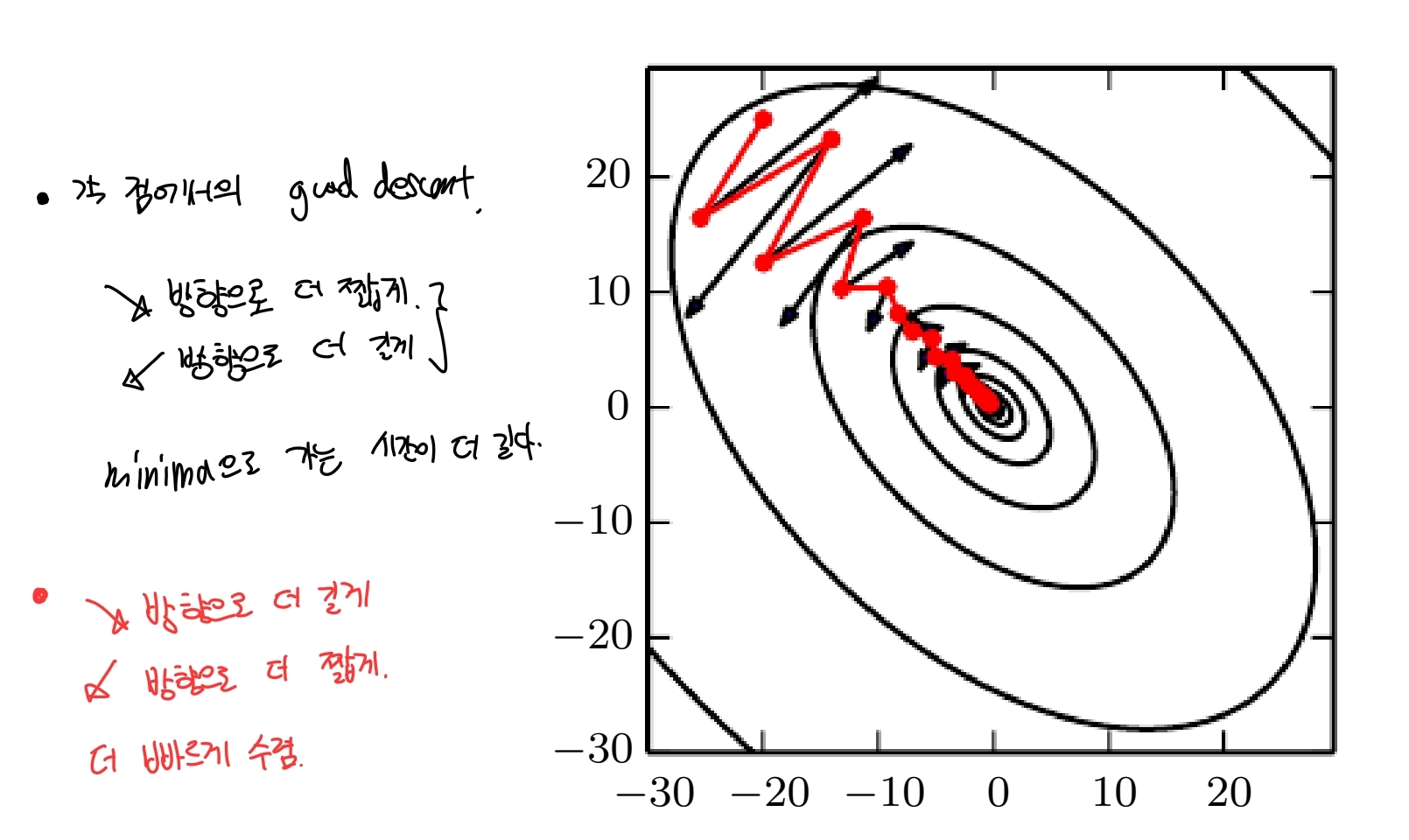
SmartSelect_20220203-224443_Samsung Notes.jpg

Goodfellow fig 8.5

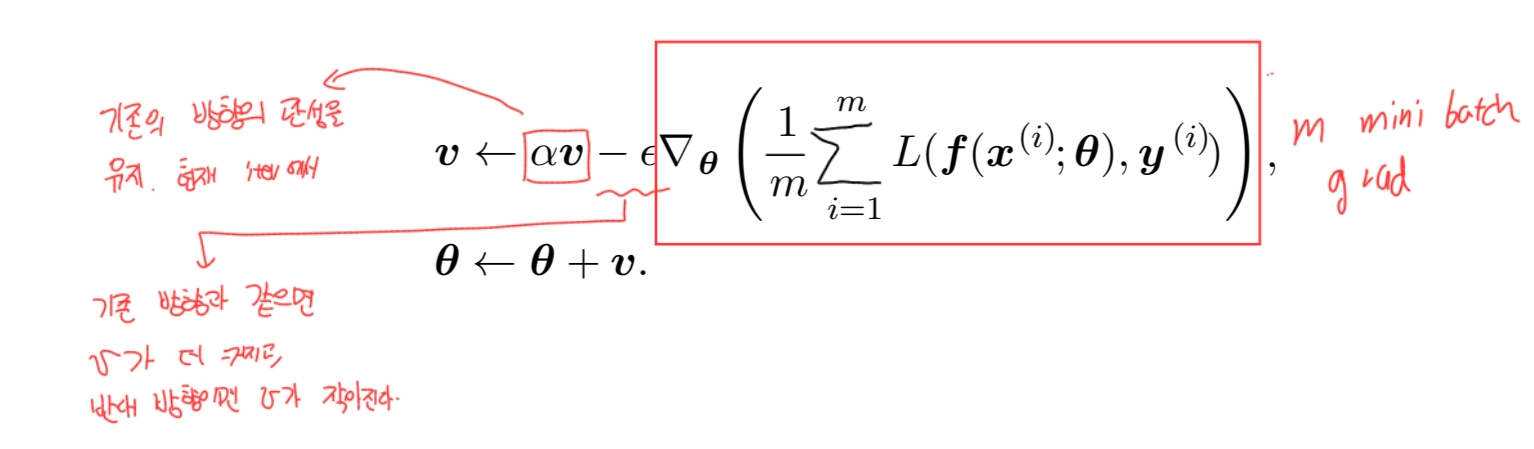
SmartSelect_20220203-225011.png

현재 iteratoin에서 기존 벡터 v의 각 원소 방향의 (+, -)에서 같은 방향이면 각 원소 값이 커지고, 반대 방향이면 작아진다. $\alpha$는 관성 파라미터! 과거의 값을 얼마나 유지할지 결정한다. 0.1, 0.5, 0.99가 자주 쓰인다고 한다.

이때 만약 매 iteration에서 grad의 값이 g으로 동일하, iteration의 값이 아주 클때(무한으로 발산할 때), 매 iteration에서 발생하는 v의 값이 동일해진다.

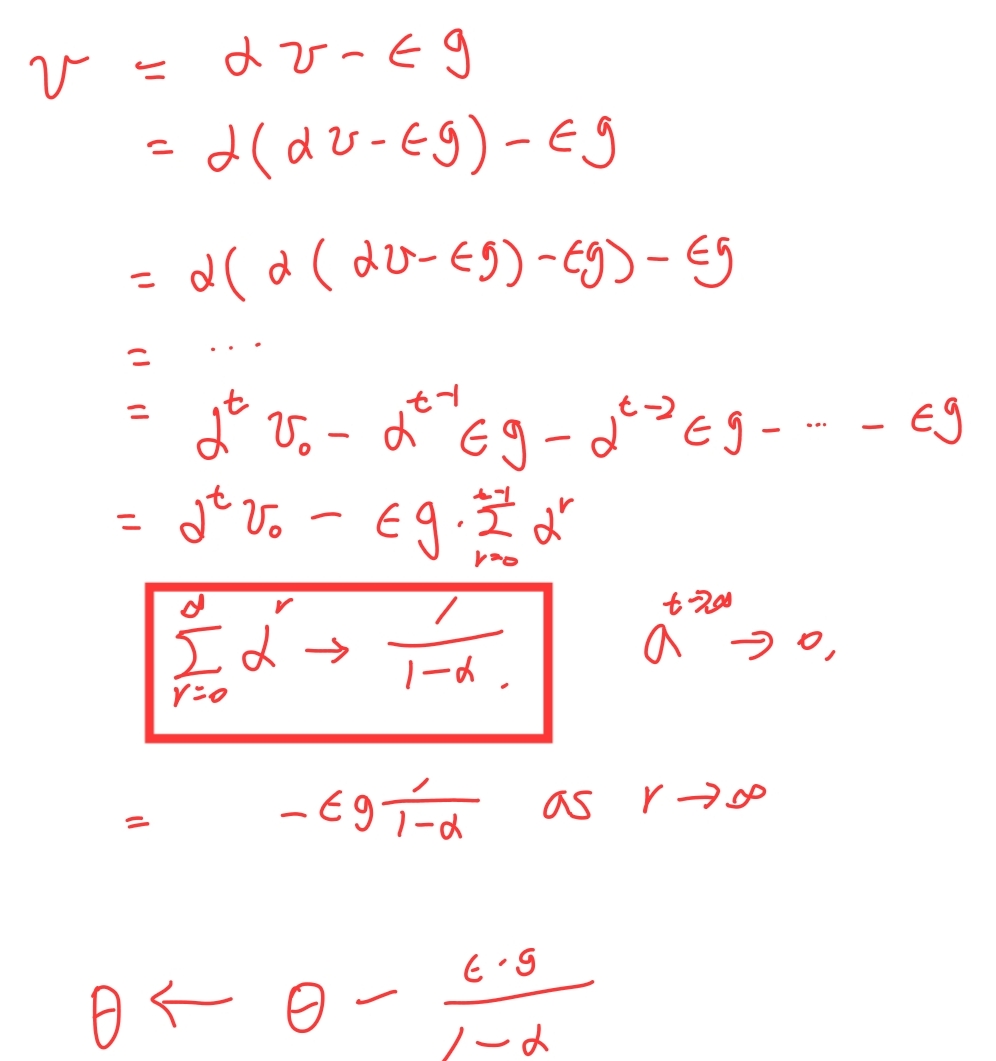
SmartSelect_20220203-225953_Samsung Notes.jpg

가중치 변경 가능

원래 모멘텀 수식

\[v \leftarrow \alpha v - \epsilon g\\ \theta \leftarrow \theta + v\\\]

직관적인 의미는 동일하게 유지하면서, 과거에 가중치를 두고 현재의 grad 값을 그래도 합치는 의미 대신에, 현재 값에도 가중치를 넣는다고 바꾸면 이렇게도 쓸 수 있음.

\[v \leftarrow \alpha v - (1 - \alpha )\epsilon g\\ \theta \leftarrow \theta + v\\\]

용법

dataloader = DataLoader(dataset, batch_size= 1, shuffle=True)
optim = SGD(params, lr = e_0, momentum = 0.99, ...)
for i = 0 to 100
	inputs, classes = next(iter(dataloader))
	outputs = model(inputs)
  loss(outputs, classes).backward()
	optim.step()

AdaGrad & RMS_PROP

이론

모멘텀이 관성을 사용해서 기존의 grad와 같은 방향이면 더 많이 쭉쭉 나가는 방법을 사용했다면, 너무 과하게 grad가 나오면 이걸 break하는 방법도 발전했다. 대표적인 것이 AdaGrad이다. 그런데 이 방법은… 이전 시점의 모든 grad을 모두 더한 값으로 각 방향의 grad가 너무 많이 이동했는지를 파악한다. 그래서 현재 위치에서 global minima으로 갈때의 특성을 고려하지 못한다. 그래서 이 방법에서 현재 상태를 더 많이 반영하기 위해서 exponential weight average을 적용한 것이 RMS_PROP이다.

AdaGrad: for each iteration,

\[r \leftarrow r + g \odot g\\ \triangle \theta \leftarrow -\frac{\epsilon}{\delta + \sqrt r} \odot g \\ \theta \leftarrow \theta + \triangle \theta\]

r: grad 각 방향의 history

e: 고정된 lr

$\delta$: 0으로 나눔 방지 작은 값. 보통 $10^{-7}$

각 iteration에서 grad을 element wise으로 곱한다. 각 방향의 grad 값을 제곱함. 이 값을 sqrt한 것이 분모로 간다. 즉, 각 방향의 값이 클수록 $\theta$ 값이 작아진다. 그래서 각 방향의 history에서 grad 이동 값이 컸으면 그만큼 break을 건다는 말임.

그래서 이 방법에서 현재 상태를 더 많이 반영하기 위해서 exponential weight average을 적용한 것이 RMS_PROP이다. 과거 history을 저장하는 r에서 가중평균을 건다.

RMS_PROP: for each iteration,

\[r \leftarrow \rho \cdot r + (1 - \rho) \cdot g \odot g\\ \triangle \theta \leftarrow - \frac{\epsilon}{\sqrt{\delta + r}} \odot g \\ \theta \leftarrow \theta + \triangle \theta\]

r: grad의 각 방향 history. 전체 history와 바로 이전 시점의 grad의 가중 평균이 적용됨.

e: 고정된 lr

$\delta$: 0으로 나눔 방지 작은 값. 보통 $10^{-6}$

Adam

이론

Adam은 break을 거는 RMS_prop과 관성을 사용한 momentum을 혼합한 방식이다. 만약 weight decay을 건다면, loss에 L2 normalization을 적용한다. 그래서 grad을 구하면 $\lambda \theta$ 이 추가 됨.

Untitled

momentum의 관성과 지수 평균의 bias correction

\[m \leftarrow \rho_1 m - (1 - \rho_1 ) \cdot g\\ \hat{m} \leftarrow \frac{m}{1 - \rho_1^t}\]

rms_prop의 break과 지수 평균의 bias correction

\[v \leftarrow \rho_2 \cdot v + (1 - \rho_2) \cdot g \odot g\\ \hat{v} \leftarrow \frac{v}{1 - \rho_2^t}\]

최종 grad와 업데이트

\[\triangle \theta \leftarrow -\frac{\epsilon}{\delta + \sqrt{ \hat v}} \odot \hat m \\ \theta \leftarrow \theta + \triangle \theta\]

AdamW

Adam이 일부 task에서 generalization performance가 잘 안나옴. 그럼 우리는 regularization을 걸겠지? 근데 adam에서 그냥 grad에 regularization을 걸면… sqrt으로 정규화를 하구… (논문에서는 차원이 안맞아서…) 그래서 실제 regularization 보다 작은 값만 적용이 됨. 그래서 목표로 하는 regularization 상수 labmda을 유지하기 위해… loss에 L2을 걸어서 regularization을 하는대신, 파라미터를 업데이트할 때 lambda을 걸어서 weight decay을 해준다. pytorch 구현에서는, 미리 wegith decay을 적용하고, 거기에서 추가로 grad 값으로 업데이트를 해줌.

Untitled

용법

dataloader = DataLoader(dataset, batch_size= 1, shuffle=True)

beta1, beta2 = 0.9, 0.999 # beta1: momentum, beta2: rms_prop break momentum
eps = 1e-08 # eps for float number to prevent zero divide error

#adam: L2 normlalization을 사용해서 lambda 값이 온전히 적용되지 않는다.
optim = AdamW(params, lr = e_0, betas=(beta1, beta2), eps=eps, weight_decay=0, amsgrad=False)

#adamW: L2 대신에, param update에서 로 lambda을 적용한다.
optim = AdamW(params, lr=e_0, betas=(beta1, beta2), eps=1e-08, weight_decay=0.01, amsgrad=False)

# what scheduler for adam?
scheduler = LambdaLR(optim, 
										lr_lambda=lambda_func(lambda_func)
						)

epoch = 100
for i in range(epoch):
	inputs, classes = next(iter(dataloader))
	outputs = model(inputs)
  loss(outputs, classes).backward()
	optim.step()
	scheduler.step()

learning rate

https://hiddenbeginner.github.io/deeplearning/paperreview/2020/01/04/paper_review_AdamWR.html

https://towardsdatascience.com/https-medium-com-reina-wang-tw-stochastic-gradient-descent-with-restarts-5f511975163

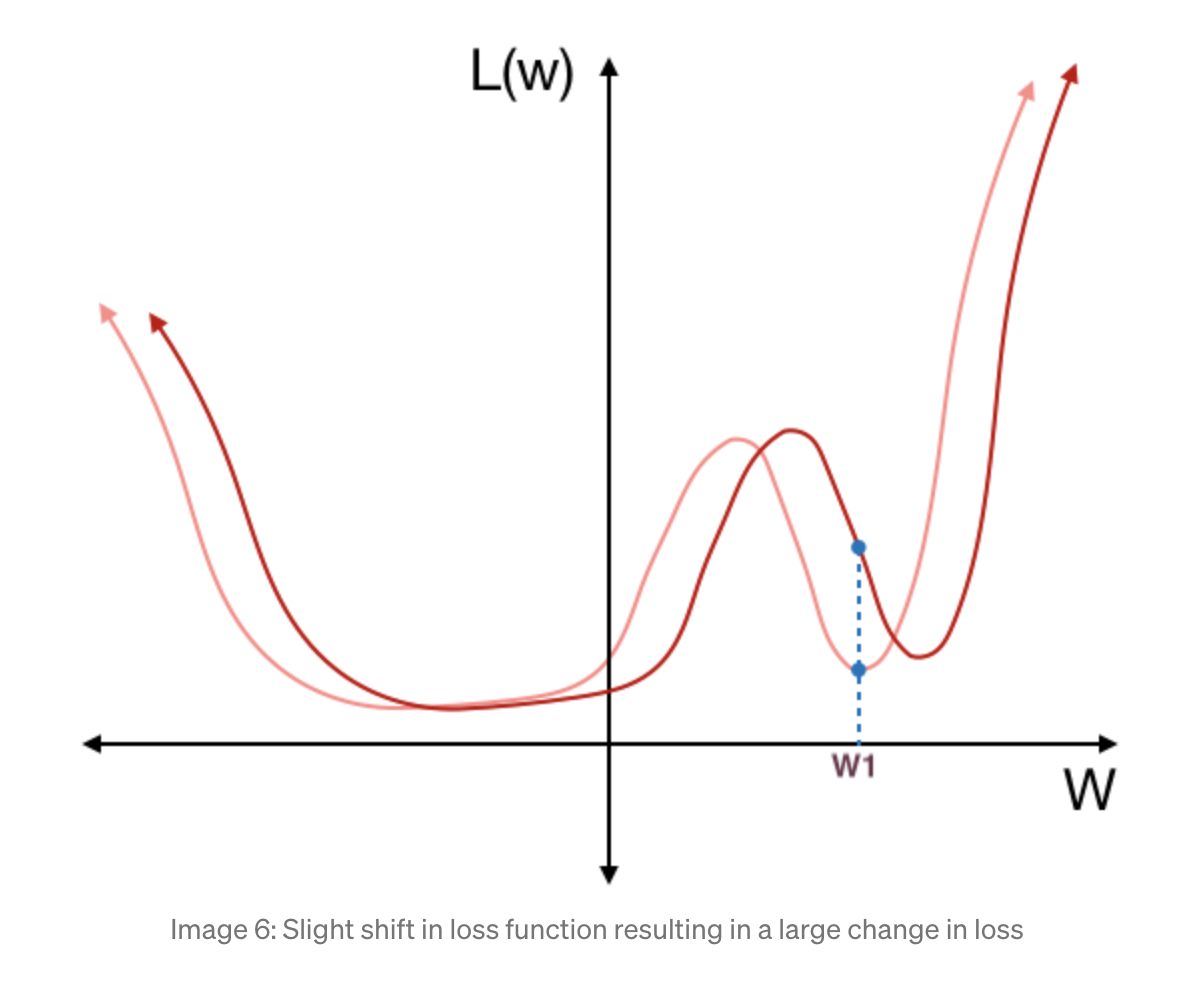
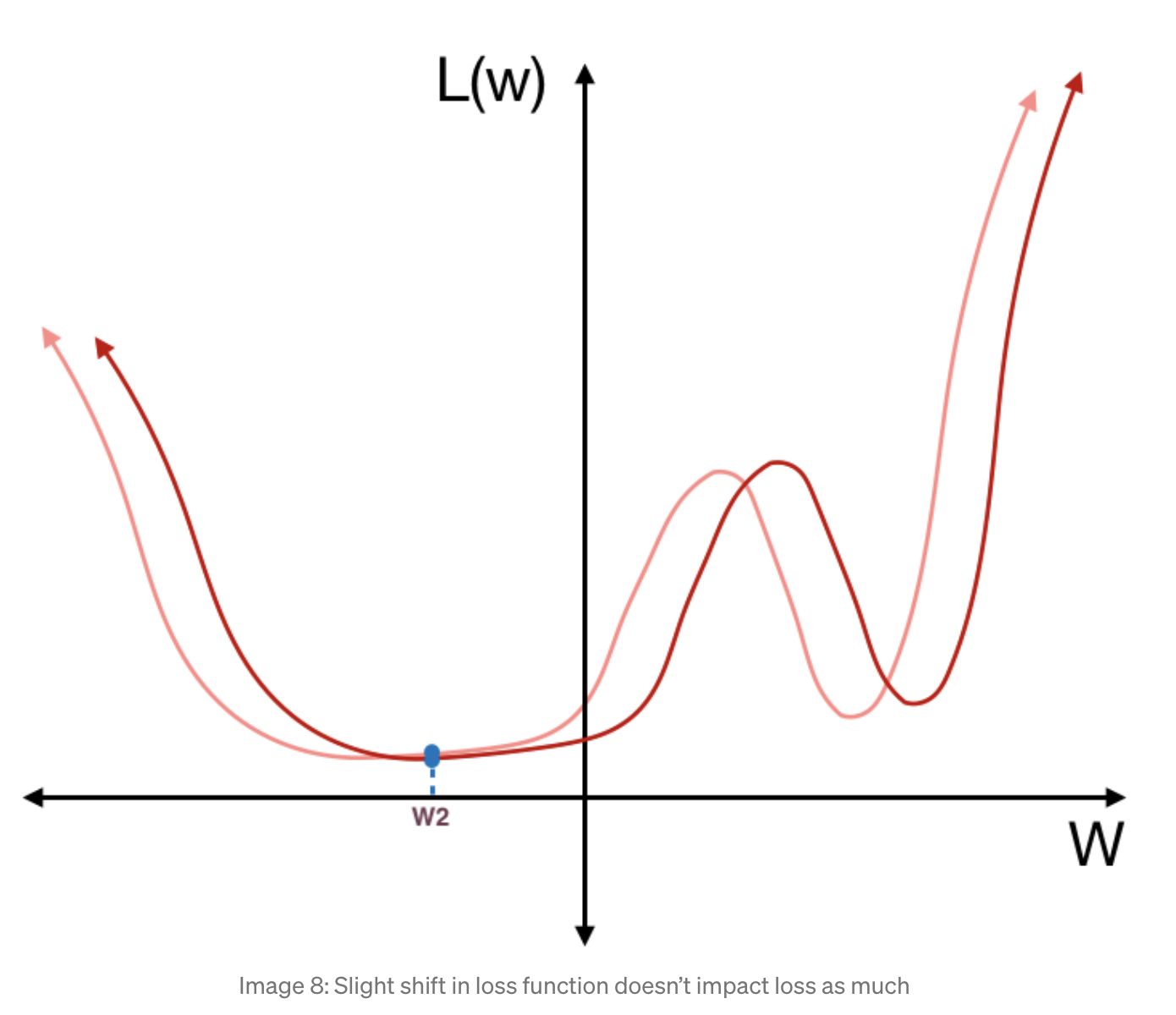
Untitled

Untitled

learning rate을 다시 증가시키는 lr 스케줄러들이 있음. 이 그림 하나로 설명 가능! generalization이 잘 되는게 사실 모든 학습의 최종 목표임. 이 loss을 보면 local minima가 두 부분이 있음. 오른쪽 부분 w1으로 학습이 되면, test data가 분포가 달라지면 갑자기 loss가 확 차이가 남. 반면 w2으로 학습이 되면 별 차이가 안나고 generalization이 잘 됨. 그래서 w1으로 떨어졌을 경우에서 빠져나오기 위해서 중간에 확 키운다. epoch이 증가하면서 loss가 커졌다 작아졌다 하게 되겠지만, 그러면서 가장 작은 loss을 보이는 곳에서 학습을 멈추면 된다!

**CosineAnnealingLR**

cosine 주기로 lr을 다시 상승시킴. 적당한 선에서 끊어야 local minima 탈출

torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=- 1, verbose=False)

from torch.optim.lr_scheduler import CosineAnnealingLR
import torch

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
scheduler = CosineAnnealingLR(optimizer, T_max=10, eta_min=0)

T_max: 변동 주기. 여기서 10 마다 최저를 찍고 다시 최대로 올라감.

eta_min: 최저 lr. 여기서 0이 최저

최대 lr은 initialLR

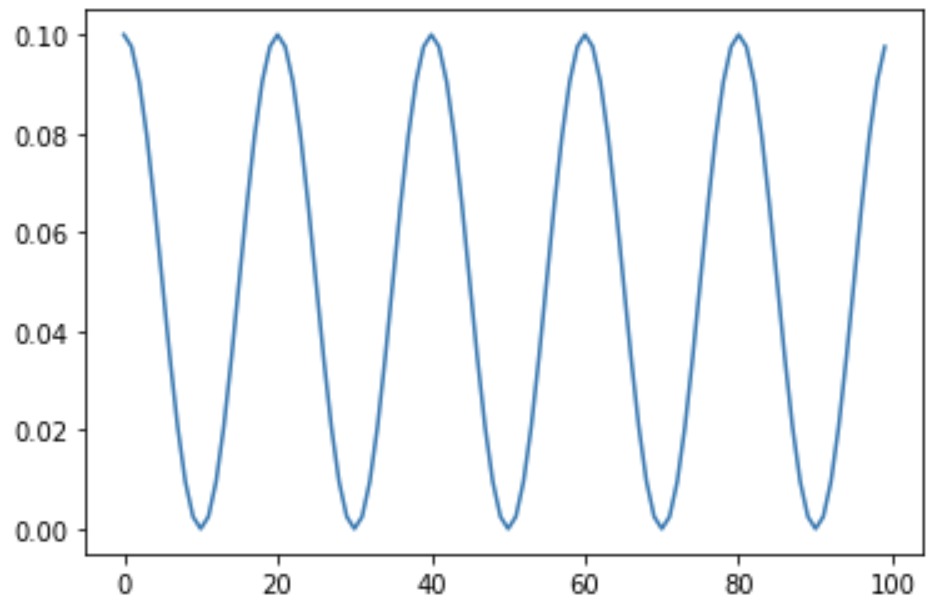
Untitled

**CosineAnnealingWarmRestarts**

lr이 다시 올라가는 것은 비슷하지만, 급격하게 올라감. local minima 탈출!

torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=- 1, verbose=False)

T_0: 최저점을 찍는 첫 주기

T_mult: 두번째 주기부터 T_mult 값을 곱함

eta_min: 최저 lr

최고 lr은 initial lr

inital lr 0.1, min_lr = 0.01, 첫 주기 10, 주기 mult =1 으로 동일 주기 반복.


from torch.optim.lr_scheduler import CosineAnnealingWarmRestarts

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
scheduler = CosineAnnealingWarmRestarts(optimizer, T_0=10, T_mult=1, eta_min=0.01, last_epoch=-1)

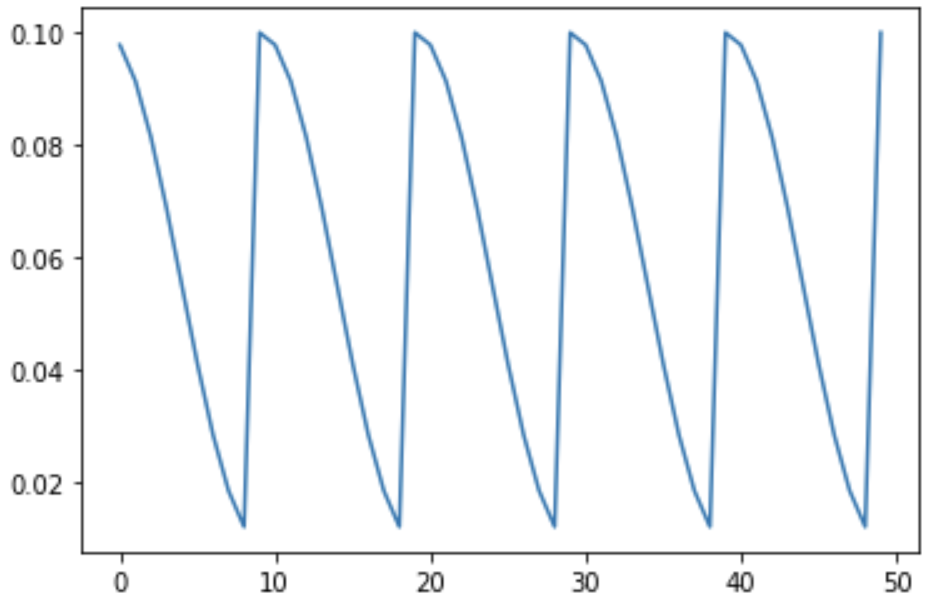
Untitled

initial lr = 0.1, min_lr = 0.01, 첫 주기 10, 주기 mult =2으로 늘어나는 것 확인

from torch.optim.lr_scheduler import CosineAnnealingWarmRestarts

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
lr_sched = CosineAnnealingWarmRestarts(optimizer, T_0=10, T_mult=2, eta_min=0.01, last_epoch=-1)

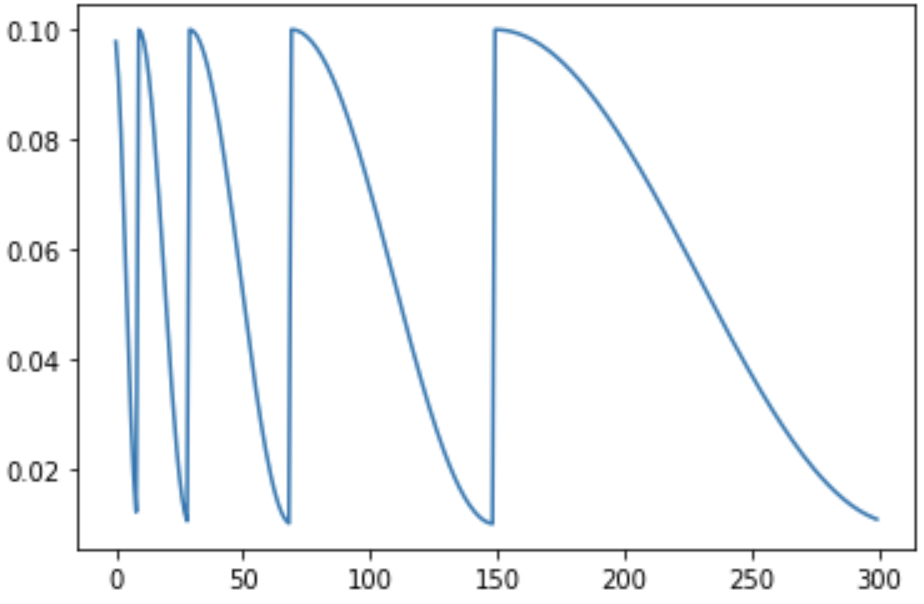
Untitled

Comments

You May Also Enjoy