Binary-Classification-Cross-Enropy-Implementation
Binary Classification Cross Enropy Implementation
What I knew
- binary cross entropy equation
- 딥러닝에 적용하면
케라스에서 구현한 식은…?
케라스에서 BCE을 구현할 때 식 그대로가 아니라 더 간다한 형태로 만든 것으로 구현한다.
- keras에서 activation function이 sigmoid일 때 binary classfication cross entropy을 구현한 식(one example)
Loss = max(logits, 0) - logits * labels + log(1 + exp(-abs(logits)))
왜 이렇게? 원래 식을 다시 살펴보자.
\[l = y_i \cdot \log{\hat{y_i}} + (1-y_i) \cdot \log{(1 - \hat{y_i})}\]실제 y값에서 틀린 예측값을 내놓을 수록 Loss 함수가 무한대로 치솟는다. 1인데 0에 가까운 hat y을 예측했다고 해보자.
\[l = \log{\hat {y_i}} \simeq \log 0 \to -\infty\]반대로 0인데 1으로 예측해도 마찬가지.
\[l = \log{(1-\hat {y_i})} \simeq \log 0 \to -\infty\]우리의 콤퓨타는… float64에서 나타낼 수 있는 수가 한정되어 있음… 로그 함수에서는 0에 가까워 질수록 훨씬 가파르게 값이 쭉쭉 내려감. numerical overflow error 뜨기 딱 좋음.
y을 이리저리 바꾸면…
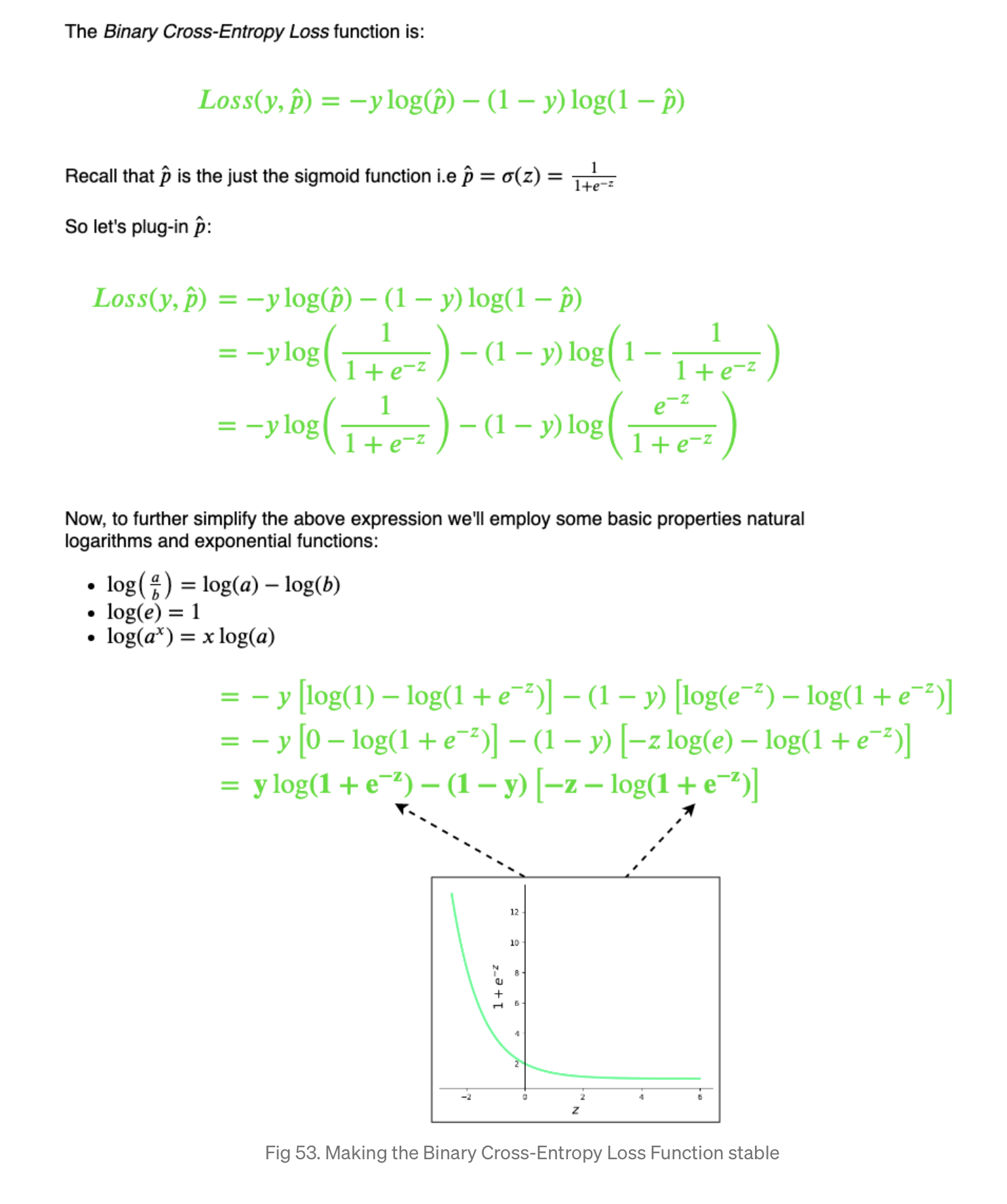
from the reference below

from the reference below
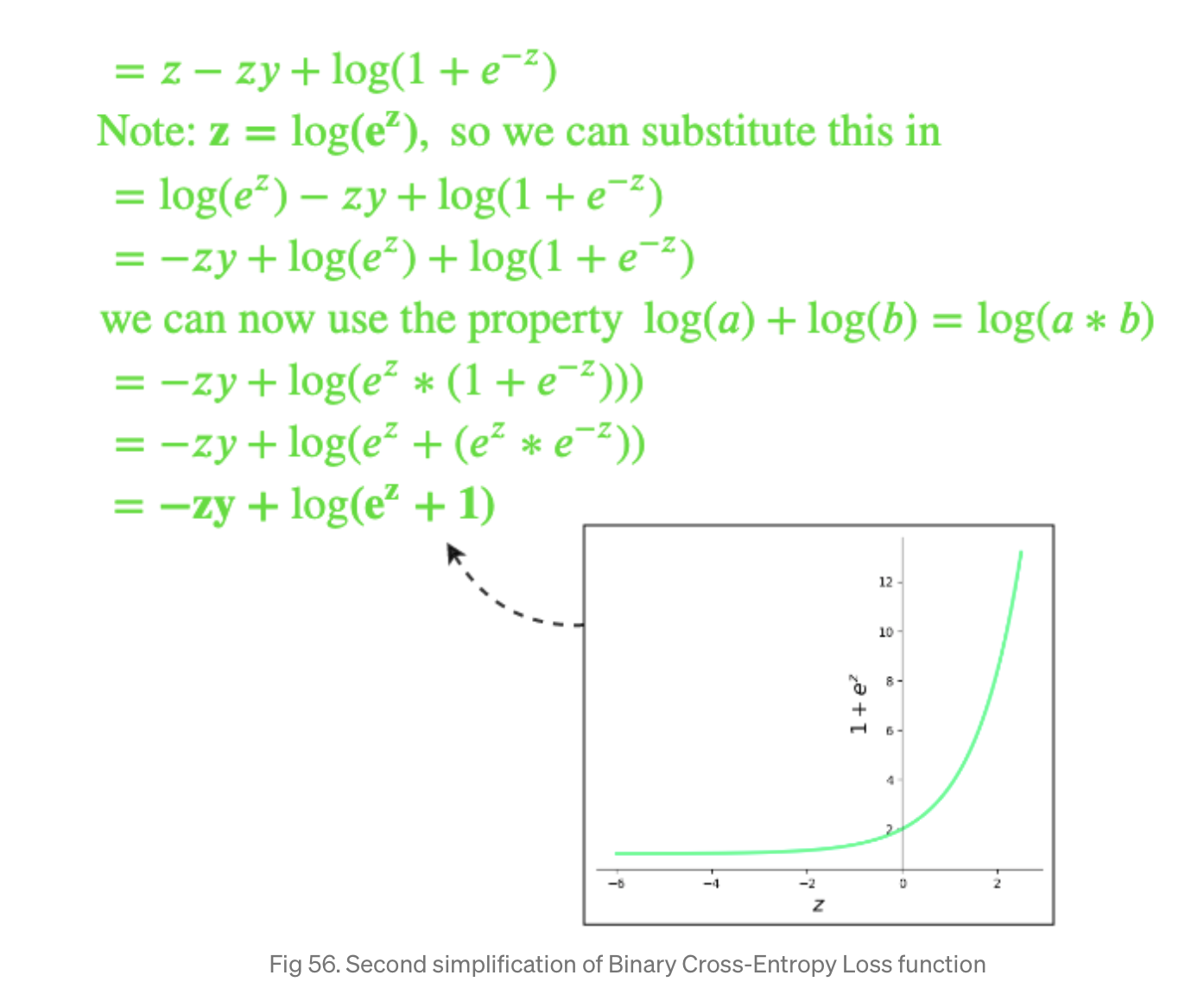
from the reference below
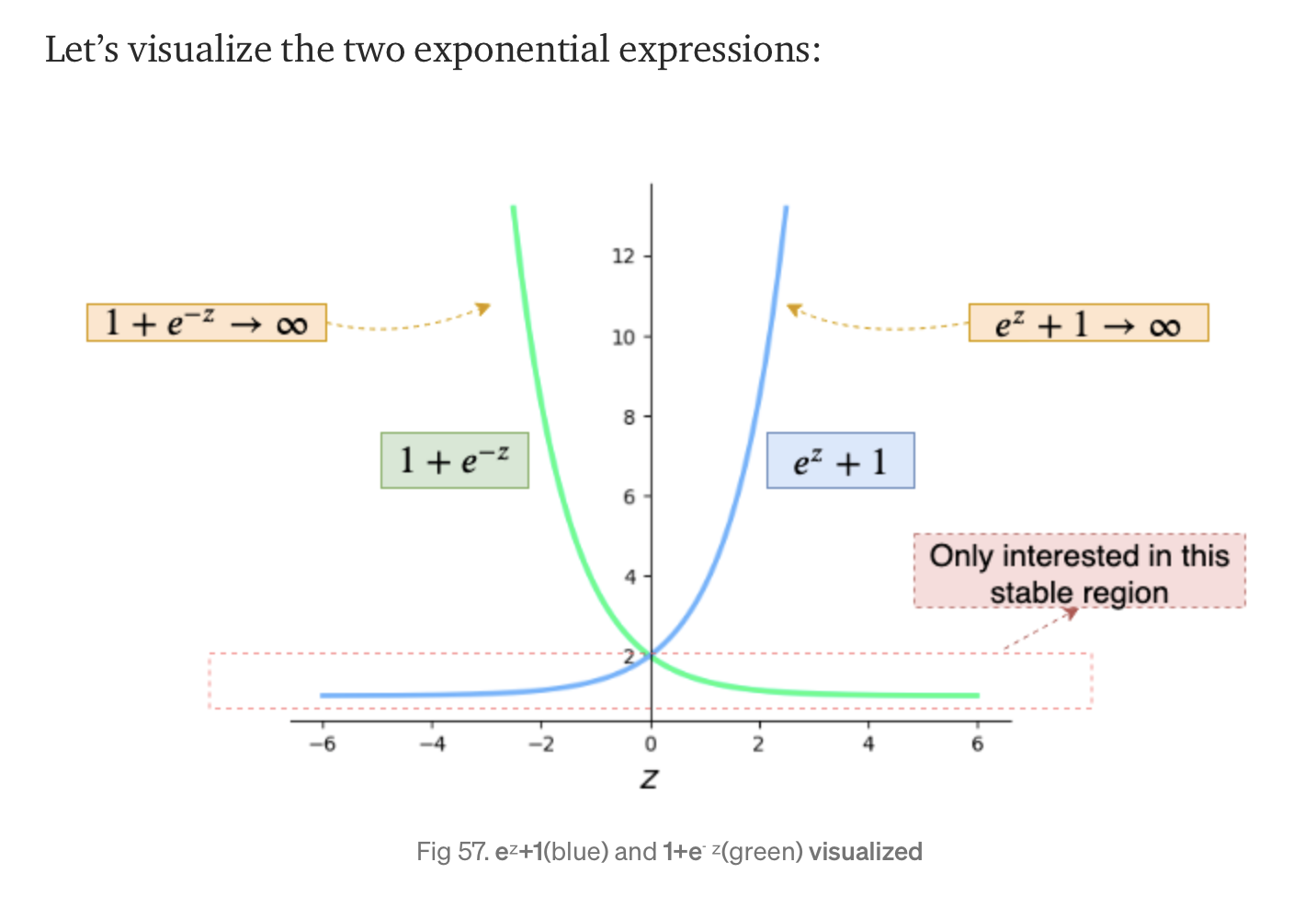
from the reference below
최종적으로
\[l = -zy + \log(e^z + 1)\]혹은
\[l = z -zy + \log(1 + e^{-z})\]이렇게 z으로 Loss Function을 나타낼 수 있게 됨. 그런데 표현하느냐에 따라서 z값이 0보다 크냐 작냐에 따라서 $\log(e^z + 1)$ 혹은 $\log(1 + e^{-z})$가 무한대로 치솓게 됨.
예를 들어
\[l = -zy + \log(e^z + 1)\]을 사용했을 때 마지막 레이어에서 z가 0보다 조금만 커져도 $l$이 무한대로 치솓음. 반대로
\[l = z -zy + \log(1 + e^{-z})\]을 사용했을 때 z가 0보다 조금만 작아도 $l$이 무한대로 뛰어오른다…
따라서 z가 무한대로 치솓지 않는 영역만 사용하자!
z가 0보다 작을 때 $l = -zy + \log(e^z + 1)$을 사용하고 0보다 클 때 $l = z -zy + \log(1 + e^{-z})$을 사용한다.
\[l = \begin{cases} -zy + \log(e^z + 1) \text{ if } z < 0\\ z -zy + \log(1 + e^{-z}) \text{ if } z> 0\\ \end{cases}\]이를 하나로 나타내면
\[max(z,0) -zy + \log{(1 + e^{-|z|})}.\]짠!
케라스 문서도 뒤져보자.
@tf_export(v1=["nn.sigmoid_cross_entropy_with_logits"])
def sigmoid_cross_entropy_with_logits
주석에 이렇게 나옴
For brevity, let `x = logits`, `z = labels`. The logistic loss is
z * -log(sigmoid(x)) + (1 - z) * -log(1 - sigmoid(x))
= z * -log(1 / (1 + exp(-x))) + (1 - z) * -log(exp(-x) / (1 + exp(-x)))
= z * log(1 + exp(-x)) + (1 - z) * (-log(exp(-x)) + log(1 + exp(-x)))
= z * log(1 + exp(-x)) + (1 - z) * (x + log(1 + exp(-x))
= (1 - z) * x + log(1 + exp(-x))
= x - x * z + log(1 + exp(-x))
For x < 0, to avoid overflow in exp(-x), we reformulate the above
x - x * z + log(1 + exp(-x))
= log(exp(x)) - x * z + log(1 + exp(-x))
= - x * z + log(1 + exp(x))
Hence, to ensure stability and avoid overflow, the implementation uses this
equivalent formulation
max(x, 0) - x * z + log(1 + exp(-abs(x)))
`logits` and `labels` must have the same type and shape.
리턴값
return math_ops.add(
relu_logits - logits * labels,
math_ops.log1p(math_ops.exp(neg_abs_logits)),
name=name)
느낀점 : 좋게 표현해서… 과학자들은 괴짜들이다.
reference
https://rafayak.medium.com/how-do-tensorflow-and-keras-implement-binary-classification-and-the-binary-cross-entropy-function-e9413826da7
[1] https://towardsdatascience.com/nothing-but-numpy-understanding-creating-binary-classification-neural-networks-with-e746423c8d5c
[2] https://github.com/tensorflow/tensorflow/blob/1cf0898dd4331baf93fe77205550f2c2e6c90ee5/tensorflow/python/ops/nn_impl.py#L112

Comments