BackPropagation-step-by-step
Stanford CS229 DNN
dW
1개의 원소로 편미분.

W_i의 의미: i번째 z노드에 모든 x벡터가 weighted sum, 내적된다. 따라서 W_i으로 미분하면, $J \leftarrow z_i \leftarrow \text{ each } W_{ij}$의 벡터 표현이다. W_i는 row vector이므로,
\[\frac{\partial J}{\partial W_i} = [\cdots \frac{\partial J}{\partial z_i} \frac{\partial z_i}{\partial W_{ij}} \cdots ]\\ = [\cdots \frac{\partial J}{\partial z_i} x_j \cdots ]\\ = \frac{\partial J}{\partial z_i} \cdot x^T\]모든 W에 대해서 편미분하면, W_i에 대해서 편미분 값을 세로료 표현할 수 있다.
\[\begin{bmatrix} \vdots\\ \frac{\partial J}{\partial W_i}\\ \vdots \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i} \cdot x^T\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i} \\ \vdots\\ \end{bmatrix} \cdot x^T = \frac{\partial J}{\partial z} \cdot x^T\]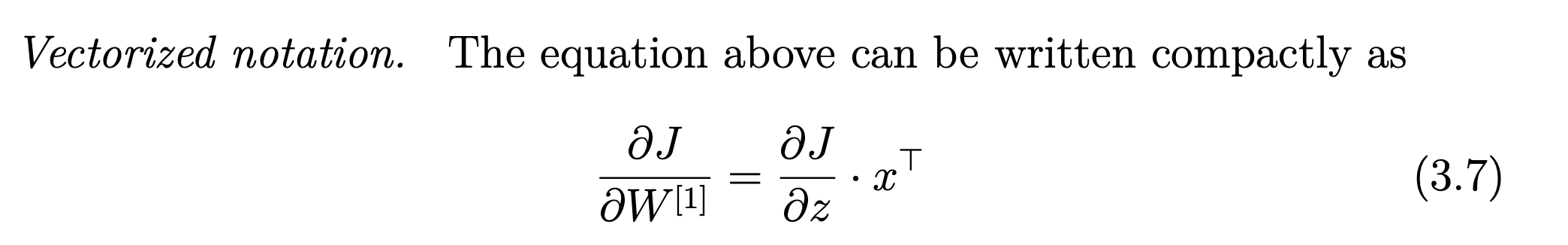
dZ
1개의 노드 $z_i$ \(\frac{\partial J}{\partial z_i} = \frac{\partial J}{\partial a_i} \frac{\partial a_i}{\partial z_i}\\ = \frac{\partial J}{\partial a_i} \frac{\partial \sigma(z_i)}{\partial z_i}\\\)
벡터 z는 column vector이다. 따라서
\[\frac{\partial J}{\partial z} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i}\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i} \frac{\partial \sigma(z_i)}{\partial z_i}\\\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i}\\ \vdots\\ \end{bmatrix} * \begin{bmatrix} \vdots\\ \frac{\partial \sigma(z_i)}{\partial z_i}\\ \vdots\\ \end{bmatrix} = \frac{\partial J}{\partial a} \odot \frac{\partial \sigma(z_i)}{\partial z}\]da
From $z = W a + b$, $a_i$는 $W$의 $W_{ji}$와 각각 곱해져서 $z_j$에 포함된다.. $J \leftarrow \text{ each } z_j \leftarrow a_i$.
\(\frac{\partial J}{\partial a_i} = \sum_j \frac{\partial J}{\partial z_j} \frac{z_j}{a_i}\\ = \sum_j \frac{\partial J}{\partial z_j} W_{ji}\\\) W에서 i번째 column 벡터와 내적. \(= < \frac{\partial J}{\partial z}, W^T_i >\\\)
원래 column 벡터인데… 앞 첨자로 표현하려면 row가 되어야 한다. 그래서 T 걸어줌. 내적 계산 자체는 $W^T_i \cdot \frac{\partial J}{\partial z}$이다. 이미 $W^T_i$가 row 라서 바로 내적.
벡터 a는 column vector이다.
\[\frac{\partial J}{\partial a} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i}\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ < \frac{\partial J}{\partial z}, W^T_i >\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ W^T_i \cdot \frac{\partial J}{\partial z}\\ \vdots\\ \end{bmatrix}\]$\frac{J}{z}$는 이미 벡터이다. 동일한 벡터를 다른 W_i벡터로 각각 내적하는 것은 matrix product 계산이다. 따라서
\[= W^T \cdot \frac{\partial J}{\partial z}\\\]Note
$J = \frac{1}{m} \sum_i \mathcal{L}( \hat y_i, y_i)$이라서 $J \in R$이다. 그리고 $a$와 $z$들은 사실 각 example i마다 가지고 있다. 따라서 $\frac{J}{a}, \frac{J}{z}$는 ith example 마다 모두 가지고 있다. J에 모든 i에 대한 summation이 걸려있지만, 다른 j번째 a으로 미분하면 다른 example의 $\frac{ \partial L(y_{i})} {\partial a} = 0$이다(Back Propagation of m examples 참조). 따라서 $\frac{J}{a}$에서 summation의 의미는 하나의 matrix에 각 column 별로 $\frac{L^i}{a}$을 stack 하는 것에 지나지 않는다.
반면 W와 b는 모든 example들이 공유하고 있는 파라미터이다.
Coursera에서 이렇게 구현했음.1 / m을 W와 b에만 곱한다. 의문1: Z와 A는? => dZ와 dA는 J가 아니라 L을 미분한 상태. 의문2: 1/m을 계속 곱하나? 누적해서? => dW와 dB는 dZ와 A만 사용한다. dZ에는 1/m이 없음. 각 layer 마다 1/m을 지속적으로 챙겨주는 것.
왜 이렇게 구현했을까? 그냥 J을 Z와 A에도 넣으면 안되었을까?
수학에서는 동일할 것 같다. 1/m sum_i L을 A으로 미분… 각 i th eg으로 미분한다음에 더하는 것과 더한 1개의 값에 미분하는 것이 같은 결과.
컴퓨터에서 미분하려면, 계산한 뒤에 대입해야 함. Z으로 Sum까지 하면 실수 되어서 미분계산 못함. L으로 벡터에서 미분하고, 나중에 더하는 것이 사실 필연적.
코드
init
dZ(L)
dW(L)
db(L)
dA(L)
grad
dA(l) = W(l).T.dot.dZ(l+1)
dZ(l) = dA(l).mult.A(l)'(Z(l))
dW(l) = 1/m * dZ(l).dot.A(l-1).T
db(l) = 1/m * sum( dZ(l) )
모든 과정을 직접 나타내보기.
호옥시 back propagation의 계산 과정이 진짜로 우리가 알고 있는 그대로 나오는지 궁금해서 한번 모든 과정을 나타내보았어요.
notaion은 Andrew Ng의 Courserg, CS229, CS230을 따랐어요! 딥러닝의 BackProgation의 모든 과정을 한걸음 한걸음 적었습니다. 벡터 미분의 다양한 방법들 중에서 index을 사용해서 진행했고, 모든 과정에서 특별한 언급이 없으면 denumerator convention을 따랐습니다.
파라미터들의 모양을 상상하면서 따라오면 쉬워요.
notation
- W의 경우 $W_i$은 row vector을 의미하고, 그외 다른 벡터 $v$의 경우 $v_i$은 element을 의미
- output을 만나는 마지막 layer은 $L$, 처음 layer은 $1$, 그 중간 layer들은 $l$으로 표기.
parameters
\[W^{[l]}, b^{[l]}, \text{for } 1 \le l \le L.\]network
layer 1 with $z^{[1]} \in R^{m_1 \times 1}, W^{[1]} \in R^{m_1 \times n}, X \in R^{n \times m}, a \in R^{m_1 \times 1}, b \in R^{m_1 \times 1}$
\[z^{[1]} = W^{[1]} \cdot X + b^{[1]}\\ a^{[1]} = g(z^{[1]})\\\]layer $l$ , $1 \lt l \lt L$ with $z^{[l]} \in R^{m_l \times 1}, a^{[l]} \in R^{m_l \times 1},W^{[l]} \in R^{m_l \times m_{l-1}}, a^{[l-1]} \in R^{m_{l-1} \times 1}, b \in R^{m_l \times 1}$
\[z^{[l]} = W^{[l]} \cdot a^{l-1} + b^{[l]}\\ a^{[l]} = g(z^{[l]}) \text{ where g is element wise function. }\\\]layer $L$ with $z \in R^{1 \times 1}, W^{[L]} \in R^{1 \times m_{L-1}}, a \in R^{1 \times 1}, b \in R^{1 \times 1}$
\[z^{[L]} = W^{[L]} \cdot a^{[L-1]} + b^{[L]}\\ a^{[L]} = g(z^{[L]})\\ o = a^{[L]}\\ \mathcal{L} = \mathcal{L}(o)\\\]cost function
\[J = \frac 1 m \sum \mathcal{L}^{(i)}\]실제 Back Propagation의 과정을 차근 차근 살펴보아요.
layer $L$
변수와 파라미터 : $z \in R^{1 \times 1}, W^{[L]} \in R^{1 \times m_{L-1}}, a \in R^{1 \times 1}, a^{[L-1]} \in R^{m_{l-1} \times 1}, b \in R^{1 \times 1}$
$\frac{\partial \mathcal{L}}{\partial W^{[L]}}$
\[\frac{\partial \mathcal{L}}{\partial W^{[L]}} = \underbrace{\delta^{[L]} \cdot (a^{[L-1]})^T}_{1 \times m_{L-1}}\]1개의 element에 대해서
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial W^{[L]}_i} & : (1 \times 1)\\ z^{[L]} & = W^{[L]} \cdot a^{[L-1]} + b^{[L]}\\ \frac{\partial \mathcal{L}}{\partial W^{[L]}_i} & = \underbrace{\frac{\partial \mathcal{L}}{\partial z}}_{1 \times 1} \underbrace{\frac{\partial z}{\partial W^{[L]}_i}}_{1 \times 1}\\ & = \delta^{[L]} \cdot a^{[L-1]}_i\\ \\ \end{aligned}\]벡터에 대해서
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial W^{[L]}} & : (1 \times m_{L-1})\\ \frac{\partial \mathcal{L}}{\partial W^{[L]}} & = \underbrace{\frac{\partial \mathcal{L}}{\partial z}}_{1 \times 1} \underbrace{\frac{\partial z}{\partial W^{[L]}}}_{1 \times m_{l-1}}\\ & = \begin{bmatrix} -\frac{\partial \mathcal{L}}{\partial W^{[L]}_i} -\\ \end{bmatrix}\\ & = \begin{bmatrix} -\delta^{[L]} \cdot a^{[L-1]}_i-\\ \end{bmatrix}\\ & = \delta^{[L]} \cdot (a^{[L-1]})^T\\ \text{where } \delta^{[L]} & = \frac{\partial \mathcal{L}}{\partial z}\\ \end{aligned}\]$\frac{\partial \mathcal{L}}{\partial z} = \delta^{[L]} : (1 \times 1)$
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial z} &: (1 \times 1)\\ \frac{\partial \mathcal{L}}{\partial z} &= \frac{\partial \mathcal{L}}{\partial o} \frac{\partial o}{\partial z} \\ \end{aligned}\]$\frac{\partial \mathcal{L}}{\partial b^{[L]}}$
\[\\ \frac{\partial \mathcal{L}}{\partial b^{[L]}} = \frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial b}\\ = \delta^{[L]}\\\]layer $l$
- $1 \le l \lt L : z^{[l]} \in R^{m_l \times 1}, W^{[l]} \in R^{m_l \times m_{l-1}}, a^{[l-1]} \in R^{m_{l-1} \times 1}, b \in R^{m_l \times 1}$
- $z^{[l]} = W^{[l]} \cdot a^{[l-1]} + b^{[l]}$
- $a^{[l]} = g(z^{[l]})$
$\frac{\partial \mathcal{L}}{\partial W^{[l]}} = \frac{\partial \mathcal{L}}{\partial z^{[l]}} \cdot (a^{[l-1]})^T$
개별 element에 대해서
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial W^{[l]}_{ij}} & : (1 \times 1)\\ \frac{\partial \mathcal{L}}{\partial W^{[l]}_{ij}} & = \underbrace{\frac{\partial \mathcal{L}}{\partial z^{[l]}_i}}_{1 \times 1} \underbrace{\frac{\partial z^{[l]}_i}{\partial W^{[l]}_{ij}}}_{1 \times 1}\\ & = \frac{\partial \mathcal{L}}{\partial z^{[l]}_i} (a_j^{[l-1]})\\ & = \delta^l_i \cdot (a_j^{[l-1]})\\ \end{aligned}\\\]벡터에 대해서
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial W^{[l]}_{i}} & : (1 \times m_{l-1})\\ \frac{\partial \mathcal{L}}{\partial W^{[l]}_{i}} & = \begin{bmatrix} -\frac{\partial \mathcal{L}}{\partial W^{[l]}_{ij}}-\\ \end{bmatrix}\\ & = \begin{bmatrix} -\delta^l_i \cdot (a_j^{[l-1]})-\\ \end{bmatrix}\\ & = \underbrace{\frac{\partial \mathcal{L}}{\partial z^{[l]}_i}}_{1 \times 1} \cdot \underbrace{(a^{[l-1]})^T}_{1 \times m_{l-1}}\\ & = \delta^l_i \cdot (a^{[l-1]})^T\\ \end{aligned}\\\]matrix에 대해서
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial W^{[l]}} & : (m_l \times m_{l-1})\\ \frac{\partial \mathcal{L}}{\partial W^{[l]}} & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial W^{[l]}_{i}}\\ | \end{bmatrix}\\ & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial z^{[l]}_i} \cdot (a^{[l-1]})^T\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ \delta^l_i \cdot (a^{[l-1]})^T\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ \delta^l_i \\ |\\ \end{bmatrix}\cdot (a^{[l-1]})^T\\ & = <\delta^l , (a^{[l-1]})^T> [\because \text{ both $\delta^l$ and $(a^{[l-1]})^T$ is a vector.}]\\ & = \delta^l \cdot (a^{[l-1]})^T\\ & = \frac{\partial \mathcal{L}}{\partial z^{[l]}} \cdot (a^{[l-1]})^T\\ \end{aligned}\\\]$\frac{\partial \mathcal{L}}{\partial z^{[l]}} = \frac{\partial \mathcal{L}}{\partial a^{[l]}} * a’^{[l]}(z^{[l]})$
- $a^{[l]} = g(z^{[l]})$
element으로 미분
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial z^{[l]}_i} & = \delta^l_i\\ & = \underbrace{\frac{\partial \mathcal{L}}{\partial a^{[l]}_i}}_{1 \times 1} \underbrace{\frac{\partial a^{[l]}_i }{\partial z^{[l]}_i}}_{1 \times 1}\\ & =\frac{\partial \mathcal{L}}{\partial a^{[l]}_i} \cdot a'^{[l]}_i(z_i^{[l]}) \\ \end{aligned}\\\]벡터로 미분
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial z^{[l]}} & = \delta^l : (m_l \times 1)\\ \frac{\partial \mathcal{L}}{\partial z^{[l]}} & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial z^{[l]}_i}\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial a^{[l]}_i} \frac{\partial a^{[l]}_i }{\partial z^{[l]}_i}\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial a^{[l]}_i} \cdot a'^{[l]}_i(z_i^{[l]}) \\ |\\ \end{bmatrix}\\ & = \frac{\partial \mathcal{L}}{\partial a^{[l]}} * a'^{[l]}(z^{[l]}) \\ \end{aligned}\]$\frac{\partial \mathcal{L}}{\partial a^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]}$
- $z^{[l]} = W^{[l]} \cdot a^{[l-1]} + b^{[l]}$
- $z^{[l+1]} = W^{[l+1]} \cdot a^{[l]} + b^{[l+1]}$
element으로 미분
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial a^{[l]}_i} & : (1 \times 1)\\ \frac{\partial \mathcal{L}}{\partial a^{[l]}_i} & = \underbrace{\frac{\partial z^{[l+1]}}{\partial a^{[l]}_i}}_{1 \times m_{l+1}} \cdot \underbrace{\frac{\partial \mathcal{L}}{\partial z^{[l+1]}}}_{m_{l+1} \times 1}\\ & = {W^{[l]}}^{T}_{i} \cdot \delta^{[l+1]} \end{aligned}\\\]기계적으로 생각하면, denumerator formation이고 denumerator가 scalar이므로 shape 맞춰주기 위해 $z^{[l+1]}$을 transpose. ${W^{[l]}}^{T}_{i} \cdot \delta^{[l+1]}$에서 $a_i$가 각 unit에 $W$의 jth column과 내적한다. 직관적으로 생각하면, 1개의 a는 여러개의 다음 노드 z에 연결된다. 따라서 전미분으로 생각해야 한다. 비용함수를 1개의 a으로 미분하면, a가 각 노드 z으로 연결되는 미분값과 각 노드 z에 대해 미분한 미분 값의 chain rule의 전미분 값으로의 합이다. 이 합이 내적으로 표현된다.
벡터로 미분
\[\begin{aligned} \\ \frac{\partial \mathcal{L}}{\partial a^{[l]}} & : (m_l \times 1)\\ \frac{\partial \mathcal{L}}{\partial a^{[l]}} & = \begin{bmatrix} |\\ \frac{\partial \mathcal{L}}{\partial a^{[l]}_i}\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ \frac{\partial z^{[l+1]}}{\partial a^{[l]}_i}\cdot \frac{\partial \mathcal{L}}{\partial z^{[l+1]}}\\ |\\ \end{bmatrix}\\ & = \begin{bmatrix} |\\ {W^{[l]}}^T_i \cdot \delta^{[l+1]}\\ |\\ \end{bmatrix}\\ & = {W^{[l]}}^T \cdot \delta^{[l+1]}\\ \end{aligned}\]summing up :
$z^{[l]} \in R^{m_l \times 1}, a^{[l]} \in R^{m_l \times 1},W^{[l]} \in R^{m_l \times m_{l-1}}, a^{[l-1]} \in R^{m_{l-1} \times 1}, b \in R^{m_l \times 1}$
$z^{[l]} = W^{[l]} \cdot a^{l-1} + b^{[l]}$ $a^{[l]} = g(z^{[l]}) \text{where g is element wise function. }$
$\frac{\partial \mathcal{L}}{\partial W^{[l]}} = \frac{\partial \mathcal{L}}{\partial z^{[l]}} \cdot (a^{[l-1]})^T$ (eq1)
$\frac{\partial \mathcal{L}}{\partial z^{[l]}} = \frac{\partial \mathcal{L}}{\partial a^{[l]}} * a’^{[l]}(z^{[l]})$ (eq2)
$\frac{\partial \mathcal{L}}{\partial a^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]}$ (eq3)
$\therefore \frac{\partial \mathcal{L}}{\partial W^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]} * a’^{[l]}(z^{[l]}) \cdot (a^{[l-1]})^T$
$\frac{\partial \mathcal{L}}{\partial b^{[l]}} = \delta^{[l]}$
general case
$z \in R^{d}, W^{[L]} \in R^{d \times m}, a \in R^{m}, b \in R^{d}$
\[\begin{aligned} z & = W a + b\\ a & = \sigma(z) \text{}\\ \mathcal{L} & = \mathcal{L}(a)\\ \\ \frac{\partial \mathcal{L}}{\partial W} & = \frac{\partial \mathcal{L}}{\partial z} a^T \\ \frac{\partial \mathcal{L}}{\partial b} & = \frac{\partial \mathcal{L}}{\partial z} \\ \frac{\partial \mathcal{L}}{\partial a} & = W^T \cdot \frac{\partial \mathcal{L}}{\partial z} \end{aligned}\]$z \in R^{d}, a \in R^{d}$
\[a = \sigma(z) \text{where $\sigma$ is element wise function.}\\ \mathcal{L} = \mathcal{L}(a)\\ \frac{\partial \mathcal{L}}{\partial z} = \frac{\partial \mathcal{L}}{\partial a} * \sigma '(z).\]pseudo code
parameters : W, b, delta
init
dZ(L)
dW(L)
db(L)
grad
dZ(l) = W(l+1).dot.dZ(l+1) * A(l)'(z(l))
dW(l) = dZ(l).dot.A(l-1).T
db(l) = dZ(l)
with m examples
- single example
- m examples
V의 차원이 (…, m)으로 유지되면서 J까지 feed forward 된다. 각 examle이 독립적으로 계산된다. 서로 엮이지 않음.
$J = \frac 1 m \sum L^i$
$\mathcal{L} \in R^{m} = [\mathcal{L^{(1)}}, \cdots, \mathcal{L^{(i)}}, \cdots \mathcal{L^{(m)}}]$
Back Propagation of m examples.
$Z^{[l]} \in R^{m_l \times m}, A^{[l]} \in R^{m_l \times m},W^{[l]} \in R^{m_l \times m_{l-1}}, A^{[l-1]} \in R^{m_{l-1} \times m}, b \in R^{m_l \times m}$
$\frac{\partial \mathcal{L}}{\partial Z^{[l]}} = \frac{\partial \mathcal{L}}{\partial A^{[l]}} * A’^{[l]}(Z^{[l]})$
a와 z는 eg 끼리 분리되어 있어서 각 eg끼리 미분하면 다른 eg에서는 0이 되어서 그냥 벡터화. W는 공유하기 때문에 내적이 발생. 1개의 $W_{ij}$으로 미분하면, m개의 eg에 대해 전미분해야 한다. 그 합이 내적에서 표현된다.
\[\begin{aligned} & \frac{\partial J}{\partial Z^{[l]}} = \frac 1 m \sum \frac{\partial \mathcal{L}^k}{\partial Z^{[l]}}\\ & \frac{\partial \mathcal{L}^i}{\partial Z^{[l]}} = \begin{bmatrix} | & | & \vdots & | & \vdots & |\\ 0 & 0 & \cdots & \frac{\partial L^i}{\partial Z^{(i)[l]}} & \cdots & 0\\ | & | & \vdots & | & \vdots & |\\ \end{bmatrix}\\ \\ \\ & \frac{\partial \mathcal{L}}{\partial Z^{[l]}} = \sum_k \frac{\partial \mathcal{L}^k}{\partial Z^{[l]}} (eq4)\\ & = \begin{bmatrix} | & \vdots & | & \vdots & |\\ \frac{\partial \mathcal{L}^1}{\partial Z^{(1)[l]}} & \cdots & \frac{\partial \mathcal{L}^i}{\partial Z^{(i)[l]}} & \cdots & \frac{\partial \mathcal{L}^m}{\partial Z^{(m)[l]}}\\ | & \vdots & | & \vdots & |\\ \end{bmatrix}\\ & = \underbrace{\begin{bmatrix} |&&|&&|\\ \delta^{(1)}&\cdots&\underbrace{\delta^{(i)}}_{m_l \times 1}&\cdots&\delta^{(m)}\\ |&&|&&|\\ \end{bmatrix}}_{m_l \times m}\\ & = \delta^{[l]}\\ \\ &\text{ since } \big [ \delta^{(i)[l]} = \frac{\partial \mathcal{L}^i}{\partial z^{(i)[l]}} = \frac{\partial \mathcal{L}^i}{\partial a^{(i)[l]}} * a'^{(i)[l]}(z^{(i)[l]})],\\ \\ & \delta^{[l]} \\ &= \underbrace{\begin{bmatrix} |&&|&&|\\ \frac{\partial \mathcal{L}^i}{\partial a^{(i)[l]}} * a'^{(i)[l]}(z^{(i)[l]})&\cdots&\underbrace{\frac{\partial \mathcal{L}^i}{\partial a^{(i)[l]}} * a'^{(i)[l]}(z^{(i)[l]})}_{m_l \times 1}&\cdots&\frac{\partial \mathcal{L}^i}{\partial a^{(i)[l]}} * a'^{(i)[l]}(z^{(i)[l]})\\ |&&|&&|\\ \end{bmatrix}}_{m_l \times m}\\ &= \frac{\partial \mathcal{L}}{\partial A^{[l]}} * A'^{[l]}(Z^{[l]})\\ \end{aligned}\\ \therefore \frac{\partial \mathcal{L}}{\partial Z^{[l]}} = \frac{\partial \mathcal{L}}{\partial A^{[l]}} * A'^{[l]}(Z^{[l]})\]$\frac{\partial \mathcal{L}}{\partial A^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]}$
\[\begin{aligned} \frac{\partial \mathcal{L}^i}{\partial a^{[l]}_i}& = {W^{[l]}}^T \cdot \delta^{[l+1]}\\ \frac{\partial \mathcal{L}}{\partial A^{[l]}} & = \begin{bmatrix} - \frac{\partial \mathcal{L}^i}{\partial a^{[l]}_i} -\\ \end{bmatrix}\\ & = \begin{bmatrix} -{W^{[l]}}^T \cdot \delta^{(i)[l+1]}-\\ \end{bmatrix}\\ & = {W^{[l]}}^T \cdot \delta^{[l+1]}\\ \end{aligned}\\ \therefore \frac{\partial \mathcal{L}}{\partial A^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]}\\\]$\frac{\partial J}{\partial W^{[l]}} =\frac 1 m \frac{\partial \mathcal{L}}{\partial Z^{[l]}} \cdot (A^{[l-1]})^T$
-
w의 경우 BPTT을 하면서 sum이 자동으로 포함되어 있음…
-
single example : $\frac{\partial \mathcal{L}}{\partial W^{[l]}}$
- m examples
$\frac{\partial J}{\partial b^{[l]}} = \frac 1 m\sum_i^m \frac{\partial \mathcal{L}^i}{\partial z} = \frac 1 m\sum_i^m \delta^{[l]}$
- 각 layer에서 모든 example에 대해 b의 값이 동일하다.
- b의 경우 내적에 포함되지 않아서… 따로 sum을 해줘야 함…
summary
$\mathcal{L} \in R^{m} = [\mathcal{L^{(1)}}, \cdots, \mathcal{L^{(i)}}, \cdots \mathcal{L^{(m)}}]$
- $\frac{\partial \mathcal{L}}{\partial A^{[l]}} = {W^{[l]}}^T \cdot \delta^{[l+1]}$
- $\frac{\partial \mathcal{L}}{\partial Z^{[l]}} = \frac{\partial \mathcal{L}}{\partial A^{[l]}} * A’^{[l]}(Z^{[l]})$
- $\frac{\partial J}{\partial W^{[l]}} = \frac 1 m\frac{\partial \mathcal{L}}{\partial Z^{[l]}} \cdot (A^{[l-1]})^T$
- $\frac{\partial J}{\partial b^{[l]}} = \frac 1 m\sum_i^m \frac{\partial \mathcal{L}^i}{\partial z} = \frac 1 m\sum_i^m \delta^{[l]}$
pseudo code
- dA = $\frac{\partial \mathcal{L}}{\partial A^{[l]}}$
- dW = $\frac{\partial J}{\partial W^{[l]}}$
- db = $\frac{\partial J}{\partial b^{[l]}}$
- dZ = $\frac{\partial \mathcal{L}}{\partial Z^{[l]}}$
init
dZ(L)
dW(L)
db(L)
dA(L)
grad
dA(l) = W(l).T.dot.dZ(l+1)
dZ(l) = dA(l).mult.A(l)'(Z(l))
dW(l) = 1/m * dZ(l).dot.A(l-1).T
db(l) = 1/m * sum( dZ(l) )

Comments