0804_math

딥러닝 학습

forward propagation

layer 1

$z^{[1]} \in R^{m_1 \times 1}, W^{[1]} \in R^{m_1 \times n}, X \in R^{n \times m}, a \in R^{m_1 \times 1}, b \in R^{m_1 \times 1}$

\[z^{[1]} = W^{[1]} \cdot X + b^{[1]}\\ a^{[1]} = g(z^{[1]})\\\]

layer $l$ , $1 \lt l \lt L$

$z^{[l]} \in R^{m_l \times 1}, a^{[l]} \in R^{m_l \times 1},W^{[l]} \in R^{m_l \times m_{l-1}}, a^{[l-1]} \in R^{m_{l-1} \times 1}, b \in R^{m_l \times 1}$

\[z^{[l]} = W^{[l]} \cdot a^{l-1} + b^{[l]}\\ a^{[l]} = g(z^{[l]}) \text{ where g is element wise function. }\\\]

layer $L$

$z \in R^{1 \times 1}, W^{[L]} \in R^{1 \times m_{L-1}}, a \in R^{1 \times 1}, b \in R^{1 \times 1}$

\[z^{[L]} = W^{[L]} \cdot a^{[L-1]} + b^{[L]}\\ a^{[L]} = g(z^{[L]})\\ o = a^{[L]}\\ \mathcal{L} = \mathcal{L}(o)\\\]

backward propagation

dW

1개의 원소로 편미분.

W_i의 의미: i번째 z노드에 모든 x벡터가 weighted sum, 내적된다. 따라서 W_i으로 미분하면, $J \leftarrow z_i \leftarrow \text{ each } W_{ij}$의 벡터 표현이다. W_i는 row vector이므로,

\[\frac{\partial J}{\partial W_i} = [\cdots \frac{\partial J}{\partial z_i} \frac{\partial z_i}{\partial W_{ij}} \cdots ]\\ = [\cdots \frac{\partial J}{\partial z_i} x_j \cdots ]\\ = \frac{\partial J}{\partial z_i} \cdot x^T\]

모든 W에 대해서 편미분하면, W_i에 대해서 편미분 값을 세로료 표현할 수 있다.

\[\begin{bmatrix} \vdots\\ \frac{\partial J}{\partial W_i}\\ \vdots \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i} \cdot x^T\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i} \\ \vdots\\ \end{bmatrix} \cdot x^T = \frac{\partial J}{\partial z} \cdot x^T\]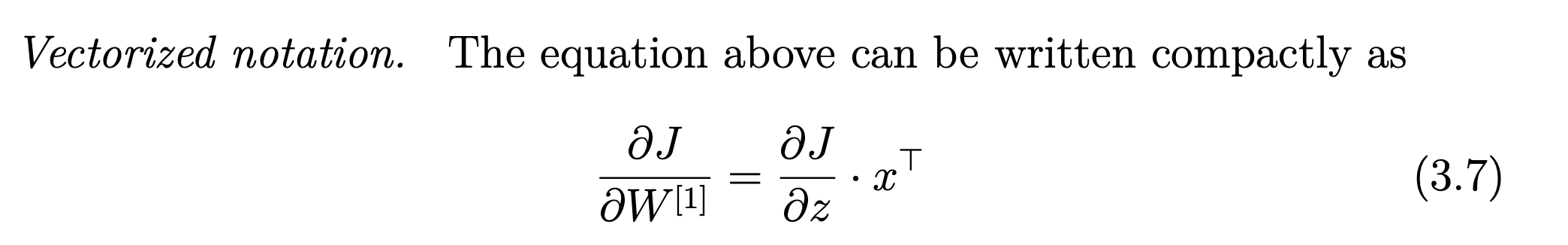

dZ

1개의 노드 $z_i$ \(\frac{\partial J}{\partial z_i} = \frac{\partial J}{\partial a_i} \frac{\partial a_i}{\partial z_i}\\ = \frac{\partial J}{\partial a_i} \frac{\partial \sigma(z_i)}{\partial z_i}\\\)

벡터 z는 column vector이다. 따라서

\[\frac{\partial J}{\partial z} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial z_i}\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i} \frac{\partial \sigma(z_i)}{\partial z_i}\\\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i}\\ \vdots\\ \end{bmatrix} * \begin{bmatrix} \vdots\\ \frac{\partial \sigma(z_i)}{\partial z_i}\\ \vdots\\ \end{bmatrix} = \frac{\partial J}{\partial a} \odot \frac{\partial \sigma(z_i)}{\partial z}\]

da

From $z = W a + b$, $a_i$는 $W$의 $W_{ji}$와 각각 곱해져서 $z_j$에 포함된다.. $J \leftarrow \text{ each } z_j \leftarrow a_i$.

\(\frac{\partial J}{\partial a_i} = \sum_j \frac{\partial J}{\partial z_j} \frac{z_j}{a_i}\\ = \sum_j \frac{\partial J}{\partial z_j} W_{ji}\\\) W에서 i번째 column 벡터와 내적. \(= < \frac{\partial J}{\partial z}, W^T_i >\\\)

원래 column 벡터인데… 앞 첨자로 표현하려면 row가 되어야 한다. 그래서 T 걸어줌. 내적 계산 자체는 $W^T_i \cdot \frac{\partial J}{\partial z}$이다. 이미 $W^T_i$가 row 라서 바로 내적.

벡터 a는 column vector이다.

\[\frac{\partial J}{\partial a} = \begin{bmatrix} \vdots\\ \frac{\partial J}{\partial a_i}\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ < \frac{\partial J}{\partial z}, W^T_i >\\ \vdots\\ \end{bmatrix} = \begin{bmatrix} \vdots\\ W^T_i \cdot \frac{\partial J}{\partial z}\\ \vdots\\ \end{bmatrix}\]

$\frac{J}{z}$는 이미 벡터이다. 동일한 벡터를 다른 W_i벡터로 각각 내적하는 것은 matrix product 계산이다. 따라서

\[= W^T \cdot \frac{\partial J}{\partial z}\\\]

Reference: Stanford cs229

확률론

데이터 공간

\((\bold x, \bold y) \sim \mathcal{D}\)

join prob $P(\bold x ,\bold y)$이 $\mathcal{D}$을 모델링한다.

What I know:

given $x$ model distirution of $y$, $P(y|x)$.

e.g. \((y|x) \sim \mathcal{N}\)

for all $x$, $P(\bold x ,\bold y)$가 $(\bold x, \bold y) \sim \mathcal{D}$을 모델링한다는 것이 직관적으로는 이해할 수 있겠음. x의 분포까지도 고려한다는 생각이 생소 함. 주어진 feature에서 어떤 확률 변수 x가 나올지도 포함되어 있음… ML에서도 P(y)는 구해도 P(x)는 잘 구하지 않았던 것 같아서… P(x)도 예측해서 유의미한 의미가 있는 영역이 있는지 궁금…

분류 문제에서 $softmax(W\phi + b)$은 데이터 $x$ 로부터 추출된 특징패턴 $\phi(x)$…

forward propagation에서 activation function 결과을 feature map으로 해석할 수 있음. 딥러닝을 kernel으로 해석… 내적, 내적, 내적…